Difference between Percentage and Percentile
What is Percentage?
A percentage is a mathematical number that is written out of a total of 100. The percent “%” sign is used to indicate that the denominator is 100.
Percentages give information about proportions and ratios. It is often easier to use and understand differences when we use percentages rather than fractions with different denominators.

Using a percentage is an easy way to standardize different quantities for comparison purposes. The percentage has therefore many applications and is used in many different situations, even in everyday life.
For instance say you want to know what proportion of children in each school are males but there are a different number of students in each school.
Clearly the only way to compare the number of males in the two schools is if you have the same total for each school.
Thus we would convert the numbers to percentages and then compare the two schools. By standardizing we now can easily see if one school has a higher proportion of male students than the other school.
Percentages can be written as ratios and decimals, so 50% is the same as 5/10 and 0.50.
Percentages are used in such areas as calculating interest rates in the financial world, to calculating student’s grades at school or college.
We can also use percentages to indicate changes in values such as increases or decreases. For instance, a student’s grades may increase from one test to another, so maybe they have improved by 10%. This is very useful as it shows change over time of some value.
It is commonly used in the banking world to indicate interest rates. Annual percentage rate (APR) is a fee that you are charged on a loan for instance.
Since percentage is so widely used it is an important concept to learn in school.
A percentage is a mathematical quantity that is not used much as a statistical quantity, although some statistical tests can analyze percentage data.
What is Percentile?
A percentile is a percentage of values found below a specific value. It is related to percentage in this way. For example say the 75th percentile on a test is 160. That means that if you scored 160 then you scored better than 75% of the people that took that same test.
A percentage can’t change value, 75% is always going to be 75/100. In comparison, a percentile can change.
Say the following year, a student scores 150 on this test, and now this is in the 75th percentile. This is because now in this year the range of student scores is different from the range of scores of the previous year.
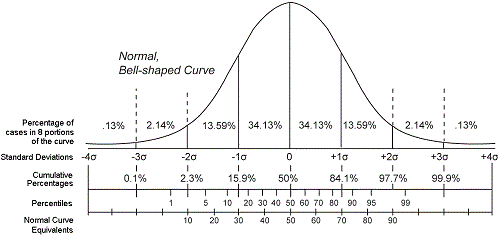
Percentiles are used in standardized tests to establish a ranking system of achievement. It is what percentile the score falls in relative to other test scores that matters. It is based on dividing up a normal distribution of values into percentiles; the most important of these are the 25th, 50th and 75th percentile.
A normal distribution is a curve of values that takes the shape of a bell. Percentiles divide this “bell” up into sections. Percentiles rely on and assume that data follows a normal distribution, which may not be the case in all situations.
The 25th and 75th percentile are also referred to as quartiles, since they represent one quarter (1/4) and three quarters (3/4) of the values, respectively.
Percentage and percentile do not necessarily represent the same quantity. For example if you take the SAT and score 60% on the test you may find you are only in the 40th percentile.
This is because it depends on how many other people scored 60% out of the total number who took the test.
The percentile is relative to the score that other people made on the test, while percentage is your individual score. Percentile is used when scoring standardized tests, and is used in statistics.
Difference between Percentage and Percentile
- Definition: Percentage is a number out of 100, while percentile is not.
- Position: Percentile is a value below which a certain percentage of values are found.
- Symbol: The symbol for percentage is the percent sign, % while percentile is indicated with xth, where x is a number, so e.g. 25th
- Quartiles: Percentiles have quartiles while percentages do not.
- Rank: Percentiles are based on ranked numbers while percentages are not.
- Decimals: Percentages can be written as decimals, percentiles can’t be written as decimals.
- Ratio: Percentages can be written as a ratio, while percentiles cannot be written as a ratio.
- Based on: A percent is based on one case, while percentile is based on a comparison of one case with all the cases in a particular situation.
- Distribution: Percentiles rely on a normal distribution, while percentages do not.
Table Comparing Percentage and Percentile
| Percentage | Percentile |
| Is a number out of 100 | Is not a number out of 100 |
| Is not a value below which a certain number of values are found | Is a value below which a certain number of values are found |
| Written as n % | Written as nth |
| Does not have quartiles | Has quartiles |
| Not based on ranked numbers | Based on ranked numbers |
| Can be written as a decimal | Can’t be written as a decimal |
| Can be written as a ratio or proportion | Can’t be written as a ratio or proportion |
| Based on one case | Based on a comparison of one case with several cases |
| Does not rely on a normal distribution | Relies on a normal distribution |
Summary on difference between percentage and percentile :
- A percentage is a number that is written out of a total of 100. It is an individual value that is indicated with the percent sign, so x %.
- Percentile is a value that is based on a comparison with other values along a normal distribution curve and is indicated as xth.
- Some percentiles are also named quartiles as they are at the ¼ and ¾ positions on the curve.
- Percentages can be written also as decimals, ratios and proportions while percentiles can’t be written in this manner.
- Difference Between Constipation and Bowel Obstruction - April 3, 2024
- Difference Between Constipation and Diarrhea - March 30, 2024
- Difference Between Cellulite and Stretch Marks - March 25, 2024
Search DifferenceBetween.net :
 Email This Post
: If you like this article or our site. Please spread the word. Share it with your friends/family.
Email This Post
: If you like this article or our site. Please spread the word. Share it with your friends/family.
1 Comment
Leave a Response
References :
[0]Barbara Illowsky, Barbara, and Susan Dean. Introductory Statistics.
[1]Barbara Illowsky, Barbara, and Susan Dean. Introductory Statistics.
[2]Houston: Rice University, 2017. Print.
[3]Lane, David M. “Percentiles”. Online Statistics Education: A Multimedia Course of Study. Rice University, 2017, http://onlinestatbook.com/2/introduction/percentiles.html
[4]University of Guelph. About percentages and percentiles. Canada: University of Guelph, 2017, Web.
[5]"Image Credit: https://commons.wikimedia.org/wiki/File:Emblem-percentage.svg"
[6]"Image Credit: https://en.wikipedia.org/wiki/Percentile_rank"


Nice recommend