Difference Between Physical Model, Mathematical Model and Real World

In general, the theoretical and scientific study of an object, a system or anything of interest centers around a model, that is, something that mimics the relevant features of the object being used for study. A model is a physical representation of an object of interest which shows how the object looks and how it works. It is often a miniature representation of the object under study. For example, when we say a working scale model of the sports arena, or a miniature model of the building or a car, we don’t refer to the actual structure or object; we only refer to a model of the actual object or structure. This is the way science develops. A model is often depicted as a mathematical representation of the object or system or process. So, how does a mathematical model differ from a physical model and how the two compare in the context of the real world? Let’s take a look.

What is Physical Model? 

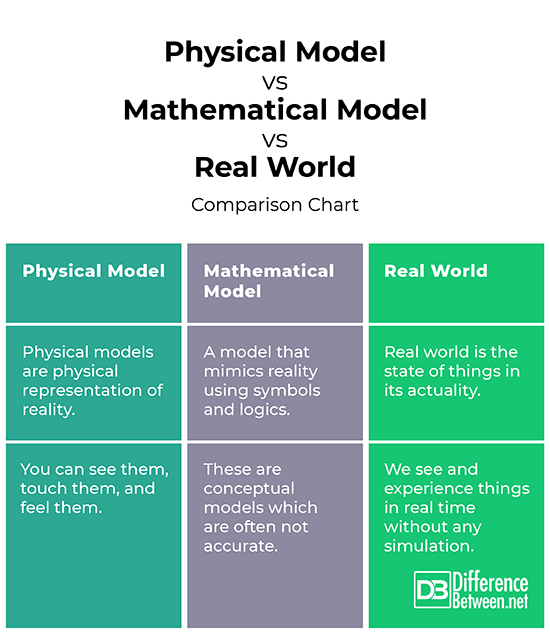
A physical model is simply referred to as a model but differs from a conceptual model. A physical model is a physical representation of the modeled system, a miniature version of the object used to study how well it performs in the real world. A physical model is a scaled-up model of the object under study which may be small or large and it’s an exact replica of the original design but smaller and its physical characteristics resemble the physical characteristics of the original object or system. Although, physical models may not seem like much or in some cases, they are often not similar, they are sufficiently real and reliable if made carefully and used correctly. The best feature of physical models is that we can see them, touch them, and feel them. And when we put them into test by applying some of the real world problems, we can expect that the same effects can be seen in the original designs or objects.

What is Mathematical Model?

A mathematical model is an abstract model that mimics reality using the language of mathematics. A model without a modifier is a mathematical model. Unlike a physical model, a mathematical model is a representation of symbols and logics instead of physical characteristics. The symbols used can be a language or a mathematical notation. A model mimics part of reality and helps us to solve problems. In the context of mathematical model, it’s not wrong to think of a system or object in general terms. Any object can serve as a system and if we have any problem related to that object, it can be solved using mathematics. So, when we want to think of a system in mathematical terms, we refer to the mathematical model of the system. Mathematical modeling is simply the best thing to do when it comes to engineering or scientific problems.

What is Real World?

Real world is the state of things as they exist in the actual world we live in, as opposed to the simulated, abstract, or theoretical realm. When we say real world, we refer to the world in general like we experience the things in real time. When we say physical models are simulation of the real world, we mean reality rather than an idea – real building, real hills, moving vehicles, and so on. The models are roughly equivalents of the real world and no matter how good they are, it’s nearly impossible to replicate every characteristic of the real world. A real world is very different from the model world in the sense that the real world refers to the events in its actuality whereas a model world is merely a human construct to better understand the real world systems.

Difference between Physical Model, Mathematical Model and Real World

Representation

 – A physical model is a scaled-up model of the object of interest which is an exact replica of the real world model created to simplify your understanding of how the product looks and performs in the real world. Physical models are physical representation of reality. A mathematical model, on the other hand, is a representation of symbols and logics instead of physical characteristics. It is an abstract model that mimics reality using the language of mathematics. Real world is the state of things in its actuality as opposed to simulated or modeled world.

Properties

 – Physical models are sufficiently real and reliable if made carefully and used correctly. They can be either small or large physical copy of the object of interest. The best feature of physical models is that we can see them, touch them, and feel them. Mathematical models are abstract, simplified mathematical constructs related to a part of reality and are designed for a specific purpose. Mathematical models are rough estimates of the real world systems which are often not accurate and data are not available all the time. Real world means reality and the things we are seeing and experiencing at any given moment. In the real world, we have real identities and physical interactions.

Physical Model vs. Mathematical Model vs. Real World: Comparison Chart

Summary

In a nutshell, the very clear distinction between the real world and the modeled world is the concept of physical form and reality. In either of the physical or mathematical model, you have no physical interaction; they are mere representation of the real world in physical construct or in mathematical terms. A physical model simply refers to a model of an object of interest which is designed in a way that its characteristics coincide with the physical attributes of the model. A mathematical model is a simplified mathematical construct related to a part of reality. A real world is the world in its existing state, in its entirety and we have real identities and physical interactions in the real world.

Sharing is caring!