Difference Between Parallel and Perpendicular

It only takes a moment to realize that lines are everywhere. As we walk, talk, and gesticulate, we generate lines wherever we go. It is fascinating because everywhere you look, there are lines. But often are we so busy, so wrapped up in ourselves that we fail to recognize that they are there. In fact, they were already there. It is not just that line-making is as ubiquitous as the use of hands and feet for gesturing and walking around respectively, but rather it’s a phenomenon which brings all the aspects of our everyday activities together into a single field of inquiry.  Lines are endless and they tend to be straight.

In mathematical terms, line is defined as a straight path that is endless. It is a set of points that extends infinitely in two directions. They are endlessly straight; they go on and on and on. Lines can be used in many different ways. We can make straight lines, we can make curved lines, and we can make wavy lines too. Some lines are short, some lines are long, some are thin, and some are thick. A line shows the outline of a shape. One type of line is called parallel means similar. In geometry, two lines are said to be parallel if they are equidistant and will never intersect. If two lines intersect at a right angle then they are said to be perpendicular. 

What is Parallel?

Ever look at the train tracks? Even though it may look like it, but the two steel rods will never intersect because they are parallel. There are many examples of parallel lines that you see everyday such as table, chair, staircase, drawer, door, and road are only a few. There are millions of examples of parallel lines around us that we see everyday yet don’t realize. Parallel lines are lines that will never meet on a plane and they are always at an equal distance apart. Imagine, what would happen if the stair steps were not parallel with each other or take the legs of a chair, for that matter? Anyone using the steps or the chair would likely fall. Two parallel lines have the same slope and they will never touch each other. However, for two lines to be parallel they must be on the same plane.

What is Perpendicular?

Lines cannot be always parallel. In fact, lines can intersect and when they do, angles are formed at their intersection point. When two lines intersect at a right angle meaning with a measure of 90°, the lines that formed those angles are said to be perpendicular. In geometry, perpendicular means at a right angle. When a line meets another line at a right angle, or 90°, perpendicularity is formed meaning both lines are perpendicular to each other. In simple terms, a line that makes a right angle with another is called a perpendicular line. For example, walls are perpendicular to the floor or when we stand upright, we stand perpendicular to the plane. Two perpendicular lines form four angles at their intersection points, all of which are equal and are at right angles.

Difference between Parallel and Perpendicular

Definition of Parallel and Perpendicular

Two non-vertical lines are said to be parallel if they are equidistant till the end of infinite lengths and has the same slope. In geometry, the lines which are equally distant from each other in all their parts and will never intersect are called parallel lines. Lines cannot be always parallel. When two intersecting lines form four angles at their intersection points, all of which are equal and at right angles, then the lines are said to be perpendicular to each other. Two lines are perpendicular when they meet at right angles.

Slope

Two lines are said to be parallel when they are equidistant from each other and will never intersect or touch. Because the lines are equally distant from each other, they have the same slope meaning the distance between the lines is same at different parts. In simple terms, the slope of two parallel lines is equal. Slope of perpendicular lines, on the other hand, are negative reciprocals of each other meaning the lines cross each other at right angle.

Representation of Parallel and Perpendicular

Here, the two lines are parallel lines and denoted as “∥”.

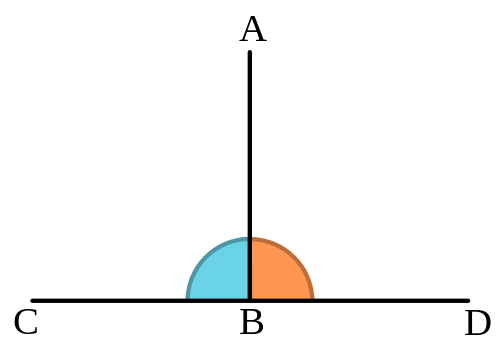
Here, the lines are perpendicular to each other and denoted as “⊥”.

Examples for Parallel and Perpendicular

There are various examples of both parallel lines and perpendicular lines all around us that we see every day. Two side of a page, rails of railways tracks, staircase railings, steps of a ladder, legs of a chair, edges of walls and ceilings, adjacent telephone poles, frames of buildings, are all examples of parallel lines in real life. Some real life examples of perpendicular lines include electric pole, corner of two walls, standing man, stop symbol, Stonehenge, bridges, tree or any standing structure that stands at 90 degrees with respect to the surface or plane.

Parallel vs. Perpendicular: Comparison Chart

Summary of Parallel Vs. Perpendicular

In a nutshell, the word parallel refers to two equidistant lines that will never intersect or touch each other at any point. Because the lines are equally distant, they have the same slope and the angle between them is zero. On the other hand, when two lines intersect at a right angle, they are called perpendicular. The two intersecting lines form four angles at their intersection points all of which are equal meaning the angles are 90 degrees. The slopes of two perpendicular lines are opposite reciprocals of each other.

Sharing is caring!