Before we get into the topic of horizontal and vertical asymptote, let’s try to understand what exactly asymptotes are and what role they play in mathematics. In projective geometry, an asymptote is a straight line that approaches a given curve arbitrarily but does not meet at any finite distance. Geometrically, a line is an asymptote of a curve y = f(x), if the distance between the line and a point ‘P’ on the curve approaches zero as x and y both tends to infinity. A graph can have one asymptote parallel to each axis. Actually, an asymptote is something that isn’t there physically – it’s more like make-believe.

An asymptote helps determine actions or the shapes of things, but it is not really a part of the graph. It is simply an imaginary line that helps you graph a rational function. As the curve approaches toward an asymptote, it gets closer and closer to the asymptote but never actually touches it. Thus, the asymptote helps determine where the graph of the function can or cannot go. That being said, there are three types of asymptotes: vertical, horizontal and oblique asymptotes. But we will only discuss vertical asymptotes and horizontal asymptotes, and see how to figure out which is what actually.

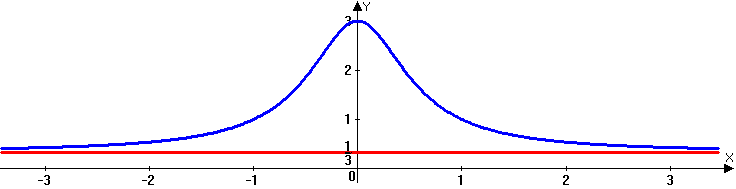
What is Horizontal Asymptote?

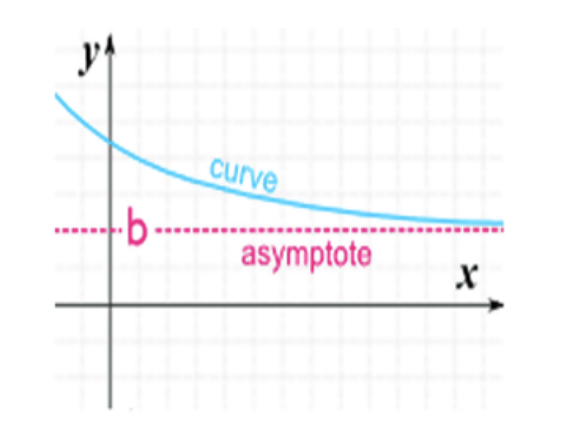
A horizontal asymptote is a constant value on a graph which a function approaches but does not actually reach. It indicates what actually happens to the curve as the x-values get very large or very small. In the graphical examples above, the curve approaches a constant value b, but never actually reaches, y = 0.

The line y = b is a horizontal asymptote of the graph of ‘f’ if f(x) —-> b as x —-> ∞ or x —-> – ∞

To find a horizontal asymptote of a rational function, the degree of the polynomials in the numerator and the denominator is to be considered.

• If the denominator has the highest variable power in the function equation, the horizontal asymptote is automatically the x-axis or y = 0.
• If both the numerator and denominator have an equal degree, take the leading coefficients of those terms with the highest power and make a fraction of them to find the horizontal asymptote
• If the numerator has the highest variable power in the function equation, the function has no horizontal asymptote; the graph will probably have an oblique asymptote.

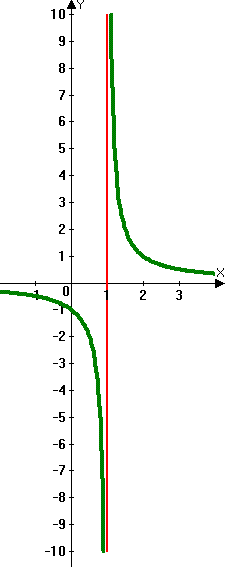
What is Vertical Asymptote?

As the denominator of a fraction can never be zero, having the variable on the bottom if a fraction can be a problem. Some domain value of ‘x’ makes the denominator zero and the function will jump over this value in the graph, creating a vertical asymptote. They are vertical lines drawn in lightly or with dashes to show that they are not part of the graph.

If the real number ‘a’ is a zero of the denominator q(x), then the graph of f(x) = p(x)/q(x), where p(x) and q(x) have no common factors, has the vertical asymptote, x = a.

Difference between Horizontal and Vertical Asymptote

Definition

– A horizontal asymptote is a constant value on a graph which a function approaches but does not actually reach. It indicates what actually happens to the curve as the x-values get very large or very small. Vertical asymptotes, on the other hand, are invisible vertical lines which correspond to the zero in the denominator of a rational fraction. They are vertical lines drawn in lightly or with dashes to show that they are not part of the graph.

Calculation

– To determine a horizontal asymptote of a rational function, the degree of the polynomials in the numerator and the denominator is to be considered. If the denominator has the highest variable power in the function equation, the horizontal asymptote is automatically the x-axis or y = 0. If both the numerator and denominator have an equal degree, then make a fraction of their coefficients to determine the horizontal asymptote equation. To determine the vertical asymptotes of a rational function, set the denominator of the fraction equal to zero.

Example

– Let’s find out the asymptotes of the function

                                                 Y =3x²+9x-21 ∕ x²-25

To find the vertical asymptotes, set the denominator of the fraction equal to zero.

                  x²-25 = 0

                  (x-5) (x+5) = 0

                  x = 5 and x = – 5

These two numbers are the two values that cannot be included in the domain, so the                     equations are vertical asymptotes. So, the two vertical asymptotes are, x = 5 and x = – 5.

Now, to determine the horizontal asymptote, look at the original equation. Here, the highest                variable power is 2. As both the numerator and the denominator have the same degree of power, make a fraction of their coefficients:

y = 3x²/x²

y = 3/1

y = 3

So, the equation of the horizontal asymptote is, y = 3.

Horizontal Asymptote vs. Vertical Asymptote: Comparison Chart

Summary of Horizontal Asymptote vs. Vertical Asymptote

An asymptote helps determine actions or the shapes of things, but it is not really a part of the graph. Vertical asymptotes mark places where the function has no domain. You solve for the equation of the vertical asymptotes by setting the denominator of the fraction equal to zero. Horizontal asymptotes, on the other hand, indicate what happens to the curve as the x-values get very large or very small. To find a horizontal asymptote, you need to consider the degree of the polynomials in the numerator and the denominator.

Sharing is caring!