Difference Between ANCOVA and Regression

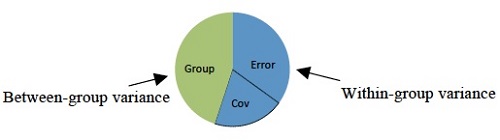
ANCOVA – Partitioning Variance

ANCOVA vs. Regression

Both ANCOVA and regression are statistical techniques and tools. ANCOVA and regression share many similarities but also have some distinguishing characteristics. Both ANCOVA and regression are based on a covariate, which is a continuous predictor variable.

ANCOVA stands for Analysis of Covariance. It is a combination of one-way ANOVA (Analysis of Variance) and linear regression, a variant of regression. It deals with both categorical and continuous variables. It is a specific statistical method for determining the extent of the variance of one variable that is due to the variability in some other variable.

ANCOVA is basically ANOVA with more sophistication and the addition of a continuous variable to an existing ANOVA model. Another form of ANCOVA is MANCOVA (Multivariate Analysis of Covariance). Moreover, ANCOVA is a general linear model that has a continuous outcome variable and two or more predictor variables. The two predictor variables are both continuous and categorical variables.

In a continuous variable, the data is quantitative and scaled, while categorical data is characterized as nominal and non-scaled. ANCOVA is mainly used to control factors that cannot be randomized but can still be calculated on an interval scale in experimental designs, while on the observational designs, it is used to erase the variable effects that change the relationship between categorical independents and interval dependents. MANCOVA also has some use in regression models where its main function is to fit the regressions in both categorical and interval independents.

ANCOVA is a model that relies on linear regression wherein the dependent variable must be linear to the independent variable. The origins of MANCOVA as well as ANOVA stem from agriculture, where the main variables are concerned with crop yields.

On the other hand, regression is also a statistical tool that is available in many variants. These variants include the linear regression model, simple linear regression, logistic regression, nonlinear regression, nonparametric regression, robust regression, and stepwise regression. Regression deals with continuous variables.

Linear regression

Regression is the relationship of a dependent variable and independent variable to each other. In this model, there is one dependent variable and one or more independent variables. There is also an effort to understand the change of the values of the dependent variable due to changes in one of the independent variants. In this situation, the other independent variants remain fixed.

In regression, there are two basic types: linear regression and multiple regression. In linear regression, the one independent variable is used to explain and/or predict the outcome of “Y” (which the variable is trying to predict). On the other hand, there is also the multiple, in which regression uses not one but two or more independent variables to predict the outcome.

The equation for both linear and linear regression is: Y = a + bX + u, while the form for multiple regression is: Y = a + b1X1 + b2X2 + B3X3 + … + BtXt + u.

In both equations, the “Y” stands for the variable that we are trying to predict; the “X” is the variable tool to predict the “Y” variable; “a” is the intercept, “b” is the slope, and “u” serves as the regression residual. It should be noted that the intercept, the slope, and the regression residual are constant.

Regression is the method for forecasting and prediction of a continuous outcome. It is the method to use for the continuous outcome, and it is based on one or more continuous predictor variables. Regression started from the field of geography whose purpose is to attempt to find the true size of the Earth.

Summary:

1.ANCOVA is a specific, linear model in statistics. Regression is also a statistical tool, but it is an umbrella term for a multitude of regression models. Regression is also the name from the state of relations.
2.ANCOVA deals with both continuous and categorical variables, while regression deals only with continuous variables.
3.ANCOVA and regression share one particular model – the linear regression model.
4.Both ANCOVA and regression can be done using specialized software to perform the actual calculations.
5.ANCOVA came from the field of agriculture, while regression originated from the study of geography.

Sharing is caring!