The difference between Paradigm and Theory

Paradigms and theories go hand in hand to explain concepts in science and assist academics in their work to define different phenomenon. The theory explains the phenomenon based on certain criteria while the paradigm provides the background or the frame that allows a theory to be tested and measured. A paradigm can have a number of theories within its framework and the paradigm acts as a reference point for the theory.  These two concepts operate with each other but have their differences. Paradigms and theories are the backbone of science and the discussion points of great masterminds like Einstein and Newton.  However, these high and lofty disciplines of science can also be applied to everyday life and help with understanding of the meaning of our environment.

What is a paradigm?

The Historian of Science, Thomas Kuhn, gave a basic definition to the meaning of paradigm.  He said ‘a paradigm is used to describe a set of concepts within a scientific discipline at any one time.’  It is a science philosophy, a set of concepts or thought patterns including theories, research and standards to contribute to a field of science or philosophy.  Paradigms are usually behind theories and allow the scientist to look at the situation and investigate the theory from every angle.  The paradigm provides the model or the pattern for the community that is investigating its theories.  It shows what is to be observed, how the observation should be conducted and begins the primary theory.  The paradigm helps show how experiments should be conducted and what equipment is best to use in that situation. It also acts as guidance to the interpretation of results.

What about a paradigm shift?

Thomas Kuhn added to his ‘Structure of Scientific Revolution’ the idea that science goes through periods of so called ‘normal science’ when existing paradigms and models dominate the scientific world.  Then revolution comes along and reality, the existing paradigm, undergoes change.  When a perception changes a paradigm shift occurs and the normal image can ‘flip’ from one state of reality to another. New paradigms become dramatic in their content when they occur in sciences that appear stable and defined. At the end of the nineteenth century it was claimed that there was nothing new in science and that scientists should just keep on measuring and updating data.  Then Albert Einstein published his paper on ‘Special Relativity’ and challenged the rules published by Newtonian Mechanics. Scientists had to make a paradigm shift.

Then there is Paradigm Paralysis!

In this situation there is a refusal to see past a model of thinking that exists and the new model or paradigm is not accepted.  A prime example of this is the rejection of Galileo’s theory of a heliocentric Solar System.  The heliocentric solar system is the theory that the Earth and planets revolve around the Sun.   This paradigm of our current solar system was vastly different in the days of the early explorers.

A paradigm is really more than a theory and several theories can be attached to one paradigm. The etymology of paradigm describes the word as Greek in origin and means, example or sample.  A paradigm is not rigid or mechanical in its approach but has a measure of flexibility.  The word paradigm has several synonyms and these help to understand the work and its usage.

Paradigm synonyms are criterion, exemplar, model, pattern and prototype to name a few.

The only noted antonym is anthisis.  This helps to makes it clear and shows that a paradigm is cooperative in its meaning with a number of synomns and virtually no antonyms.  It is visionary concept and creates a model or pattern to work from.  In the modern parts of speech context, paradigms offer descriptions of how we are in context with others. It helps with understanding how  we fit into the paradigm of our society for instance.

The study of the word paradigm in a language contest helps with further understanding of it place in language and word meanings.

Paradigm is a noun and used as an example or an accepted perspective.

Sentence with Paradigm as a noun.

The office workers accepted the paradigm of the new regulations and code of conduct within the factory and on the construction site.

Paradigms is the plural of paradigm.

The stock markets often gave out new paradigms to encourage investment during difficult times.

Paradigmatically would be the adverb usage of the word.

Sentence with paradigmatically as an adverb.

The training college let students paradigmatically practise techniques of management during their course on administration.

Paradigmatic is the adjective structure of the word.

Sentence with paradigmatic as an adjective.

There are paradigmatic clauses to the instructions on how to resolve problems in the reform school.

In a more modern context paradigms are evident in social groups and as part of events that have affected history.  The wars experienced by various nations, in particular the First and Second World War, set a pattern of behaviour on the people involved in the wars.  The friend or the foes were all affected by the paradigm of destructive human behaviour.

The individual can make changes in their lives, according to motivational speaker and author, Steven Covey by considering the paradigm of their surroundings.   He says: “If you want small changes in life work on your attitude.  But if you want big and primary changes work on your paradigm.  This would be the framework you have created for yourself that you live and move in and determines how you think and how you make decisions.  When you look at the paradigm of your life and can change that with a paradigm shift then you will be making overall changes in the way you think and live.

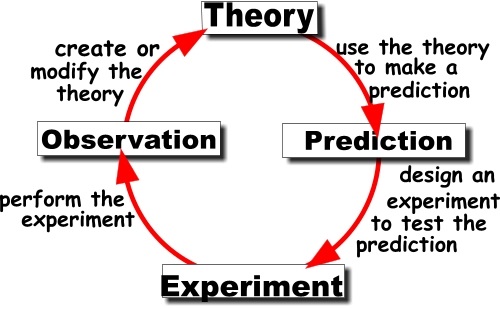
Theories, on the other hand, are the part of the paradigm that can be tested, and tried out by any number of different people.  The tested theory gives results and reaches a point of truth that can be held onto.  When people reach the same result the theory is guaranteed.  Theories bring about development in sciences and have a procedure to follow.  A procedure of experiments, scientific method and hypothesis that can be tested several times to verify the theory. A theory is an idea or several ideas used to explain facts to support a phenomenon.  The theory comes together after in-depth research and study.  It is then proven scientifically based on evidence.  Once it is proven it becomes accepted as a theory.

These well-known theories are scientific in nature.  Darwin’s theory of evolution, The Quantum theory, Special Relativity theory and Newton’s law of gravity.  Famous well known theories that are part of our universal paradigm.

There are several synonyms and antonyms that help with the understanding of the word theory.

Synonyms chosen are: doctrine, concept, dogma, conditioning and basics

Antonyms chosen are: conclusion, concrete, proof, practical.

Theory is used as a noun and a theorist is a person who develops a theory.

Theories describe the plural of theory.

Theoretical is an adjective.

A sentence with theoretical states:

The new teacher’s course is designed to be practical rather than theoretical.

Theorize is a verb used to describe how one can suggest facts or ideas while forming a theory.

A sentence with theorize:

The book written for students to study theorizes about the psychology of dreams in adolescents.

A theory can also be used as an idiom.

The decision sounds good in theory but has it been studied correctly?

Theories can also be classified as countable or uncountable.

A countable theory explains why things happen. It is the proof, the measurable explanation.

Sentence to explain: The newspaper article featured two countable theories recommended by scientists to improve the conservation of water.

The uncountable theory is a principle on which something was based.

Sentence to explain: The teaching of languages is based on practical work and the theory behind the system of language understanding.

This quote from EW Howe about a theory principle is put into simple terms:

 “A young man is a theory; an old man is a fact.”

In the final analysis it is probably safe to say that we are surrounded by paradigms and theories.  The paradigms are there to create the world we live in, the sciences, the arts, the history and everything about our universe.  The theory is there to validate the paradigms that it belongs to.  ‘The proof of the pudding is in the eating’ they say and the proof of the paradigm is in the theory that supports it – unless there is a paradigm shift and then everything could change!  A study of paradigms and theories certainly gets the reader thinking about these two words and how they work together side by side supporting one another in the universe that we live in.

Sharing is caring!