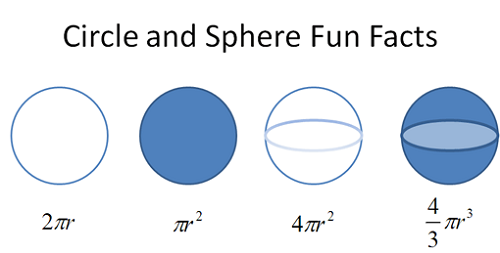Difference Between Circle and Sphere
The earth on which we live on can remind us of a circle, although not entirely a perfect one, and its’ area on which the human population is situated on, in this case, can be identified with a sphere. Therefore the geometry of circles and spheres has its broad application in every field of science, starting from, as an example – in geography, geology and geodesy. Spherical shapes can indeed be found at various places in nature, and because of the human curiosity, there is a need for their description.
What is Circle?
А circular line is a set of points in а plane with the property that all of the points of that line are on an equal distance r of a fixed point of that plane called the center of the circular line. Every line which connects the center with some point of the circular line is called a radius, and the number r is the length of the radius of that circular line. In the literature the term circle, is probably, most often used. A circle is a special case of an ellipse. Ellipse can be defined as a geometric figure of the points in the plane with a constant sum of distances between two fixed points. In case of a circle these two points (center and focus) are the same. It is known that each circle has a unique set of three points that do not lie in the same direction. These points define the triangle edges, and the center of the circumscribed circle of this triangle is in the cross section of the bisection lines. The distance from the center to any of the three given points is the radius of the circle. Another way to determine a circle through three points is to write the general form equation of the circle, in a canonical (standard) or point-slope form, to include the coordinates of the given points and to solve the system. The area of a given circle with a radius r is equal to πr2.
What is Sphere?
A space can be viewed as a set of points called elements of the space. A ball is a geometric body that is a subset of a space. It is a set of points of a plane that are on a certain distance (length) from a fixed point O. The point O is the center of the sphere, and the length that connects the center with the furthest point of the sphere is called a radius. Diameter is the line that connects two most distant edge points (the longest straight line) of the sphere and passes through its center. A circle formed by the intersection of the sphere and the plane passing through the center of the sphere is called the great circle of the sphere. All other circles formed by the intersection of the plane and the sphere are called small circles of the sphere. Through every set of three points of the sphere, there is only one circle that belongs to it.
- Area of a sphere is 4πr2;
- Volume of a sphere is 4/3πr3;
Difference Between Circle and Sphere
- Definition
A circle is a closed curved line. Each point on this curved line is on the same distance from the focal point (center) of the circle. The locus of a point that is at a fixed length from another point is known as a circle. The fixed point is a circle’s center, and the length between these two points its radius. Similarly, a sphere is also characterized as a locus of a point that is at a constant distance from a fixed point – however in three dimensional space. In simple terms – a circle is a round object in a plane, while a sphere is a round object in a space.
- Formulas
Circle, as a two-dimensional figure has only an area – πr2. Sphere, on the other hand, as a three-dimensional figure (object) has an area – 4πr2 and a volume – 4/3πr3.
- Examples
Naturally, circle and sphere are figures that can be commonly found all around us. Although a real-world example of a circle is non-existent as there isn’t a zero width object in reality – some objects can be used to describe it – such as wheels, cd’s, coins. Examples of a sphere are maybe easier to find – tennis balls, planets, oranges, globes etc.
Circle vs. Sphere
| Circle | Sphere |
| round object in a plane | round object in a space |
| two dimensional (figure) | three dimensional (object) |
| only area can be calculated | calculations include both area and a volume |
Summary
- Circles and spheres have perfect symmetry around their centers. All the points of a circle, and the furthest points of a sphere are on a fixed distance from the focal point (center). However, there are dissimilarities such as that a circle is two dimensional, while a sphere is a three dimensional object. The distance between the points that are most far away is called a diameter (and is double the radius).
- A circle has an area that can be calculated with the formula – πr2. A sphere along with an area (calculated with the formula 4πr2) has a volume that is equal to 4/3πr3.
- Real life examples of a circle cannot be find as a circle exists as a two-dimensional concept – it only got length and height and no width. However, certain objects can resemble a circle – cookies, pizza, tires … Sphere-like object examples are softball, marbles, atoms, apples and so on.
- Difference Between Thermodynamics and Kinetics - June 24, 2018
- Difference Between Welding and Soldering - June 24, 2018
- Difference Between Additive Colors and Subtractive Colors - June 20, 2018
Search DifferenceBetween.net :
Leave a Response
References :
[0]Belyaev, O. A. “Fundamentals of Geometry.” Moscow: Moscow State University, 2007. Online. http://polly.phys.msu.ru/~belyaev/geometry.pdf [Retrieved at 05.12.2017]
[1]Belyaev, O. A. “Fundamentals of Geometry.” Moscow: Moscow State University, 2007. Online. http://polly.phys.msu.ru/~belyaev/geometry.pdf [Retrieved at 05.12.2017]
[2]Koeberlein, A. “Elementary Geometry for College Students.” 6 edition. CA, U.S.A: Brooks Cole, 2014. Print
[3]Goddijn, A., Kindt, M. and Reuter, W. “Geometry with Applications and Proofs: Advanced Geometry for Senior High School, Student Text and Background Information.” Rotterdam: Sense Publishers, 2014. Print
[4]"Image Credit: https://betterexplained.com/wp-content/uploads/calculus/circle_sphere_formula.png"