Difference Between ASA and AAS
ASA vs AAS: ASA stands for “Angle, Side, Angle”, while AAS means “Angle, Angle, Side”
Geometry is fun. Geometry is all about shapes, sizes, and dimensions. Geometry is the kind of mathematics that deals with the study of shapes. It is easy to see why geometry has so many applications that relate to the real life. It is used in everything – in engineering, architecture, art, sports, and much more. Today, we will discuss triangle geometry, specifically triangle congruence. But first, we need to understand what it means to be congruent. Two figures are congruent if one can be moved onto the other in such a way that all their parts coincide. In other words, two figures are called congruent if they are the same shape and size. Two congruent figures are one and the same figure, in two different places.
It’s true than triangle congruence is the basic building block for many geometrical concepts and proofs. Triangle congruence is one of the most common geometrical concepts in High school studies. One major concept often overlooked in teaching and learning about triangle congruence is the concept of sufficiency, that is, to determine the conditions which satisfy that two triangles are congruent. There are five ways to determine if two triangles are congruent, but we are going to discuss only two, that is, ASA and AAS. ASA stands for “Angle, Side, Angle”, while AAS means “Angle, Angle, Side”. Let’s take a look at how to use the two to determine if two triangles are congruent.
What is ASA Triangle Congruence?
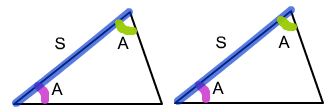
ASA stands for “Angle, Side, Angle”, which means two triangles are congruent if they have an equal side contained between corresponding equal angles. If the vertices of two triangles are in one-to-one correspondence such that two angles and the included side of one triangle are congruent, respectively, to the two angles and the included side of the second triangles, then it satisfies the condition that the triangles are congruent. Because the two angles and the included side are equal in both the triangles, the triangles are called congruent.
What is AAS Triangle Congruence?
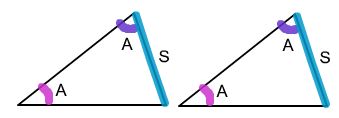
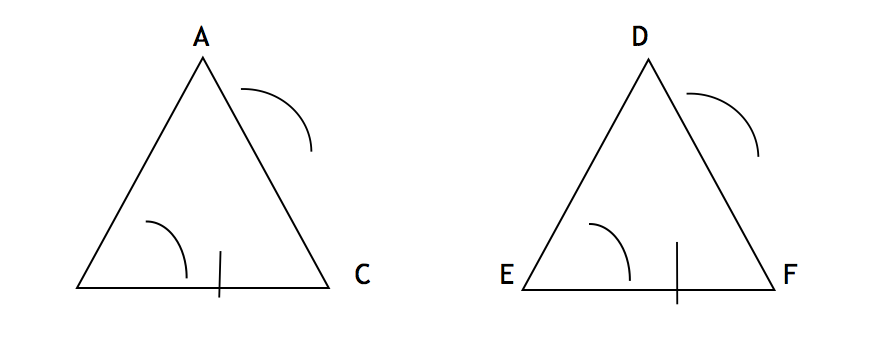
AAS stands for “Angle, Angle, Side”, which means two angles and an opposite side. AAS is one of the five ways to determine if two triangles are congruent. It states that if the vertices of two triangles are in one-to-one correspondence such that two angles and the side opposite to one of them in one triangle are congruent to the corresponding angles and the non-included side of the second triangle, then the triangles are congruent. The non-include side is the side opposite to either one of the two angles being used. In simple terms, if two pairs of corresponding angles and the sides opposite to them are equal in both the triangles, the two triangles are congruent.
Difference between ASA and AAS
Terminology of ASA and AAS
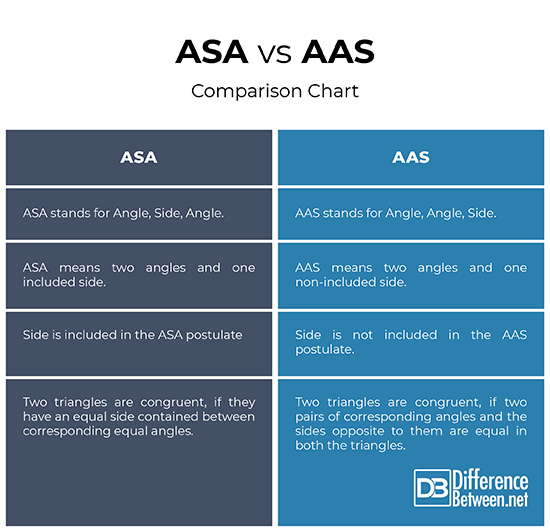
– ASA and AAS are two postulates that help us determine if two triangles are congruent. ASA stands for “Angle, Side, Angle”, while AAS means “Angle, Angle, Side”. Two figures are congruent if they are of the same shape and size. In other words, two congruent figures are one and the same figure, in two different places. While both are the geometry terms used in proofs and they relate to the placement of angles and sides, the difference lies in when to use them. ASA refers to any two angles and the included side, whereas AAS refers to the two corresponding angles and the non-included side.
Congruence
– According to ASA congruence, two triangles are congruent if they have an equal side contained between corresponding equal angles. In other words, if two angles and an included side of one triangle are equal to the corresponding angles and the included side of the second triangle, then the two triangles are called congruent, according to the ASA rule. The AAS rule, on the other hand, states that if the vertices of two triangles are in one-to-one correspondence such that two angles and the side opposite to one of them in one triangle are equal to the corresponding angles and the non-included side of the second triangle, then the triangles are congruent.
Representation
– The main difference between the two congruence rules is that the side is included in the ASA postulate, whereas the side is not include in the AAS postulate.
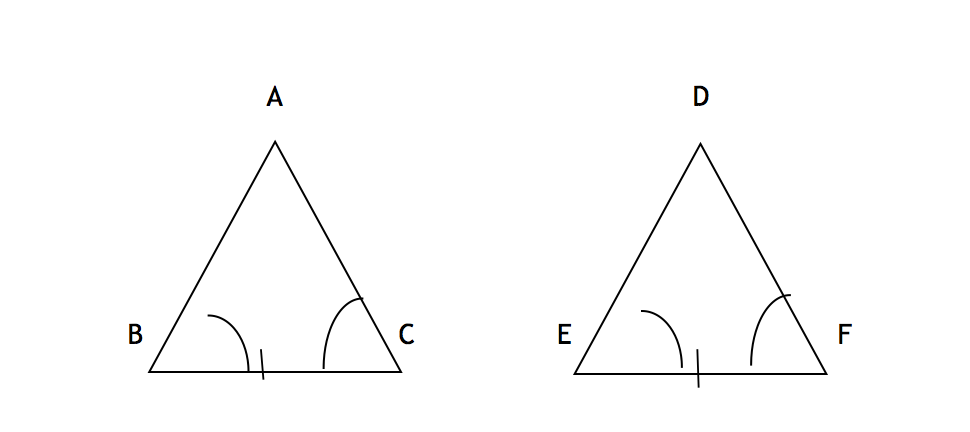
Here, two angles (ABC and ACB) and the included side (BC) are congruent to the corresponding angles (DEF and DFE) and one included side (EF), which makes the two triangles congruent, according to the ASA congruence rule.
Here, two angles (ABC and BAC) and one non-included side (BC) of the first triangle are congruent to the corresponding angles (DEF and EDF) and the non-included side (EF) of the second triangle, which makes the two triangles congruent. AC and EF can also be the non-included sides of the two triangles respectively.
ASA vs. AAS : Comparison Chart
Summary of ASA vs. AAS
In a nutshell, ASA and AAS are two of the five congruence rules that determine if two triangles are congruent. ASA stands for “Angle, Side, Angle”, which means two triangles are congruent if they have an equal side contained between corresponding equal angles. AAS refers to “Angle, Angle, Side”, which means if two pairs of corresponding angles and the sides opposite to them are equal in both the triangles, the two triangles are called congruent. While both are basically same, the main difference between the two congruence rules is that side is included in the ASA rule, whereas side is not included in the AAS rule.
- Difference Between Caucus and Primary - June 18, 2024
- Difference Between PPO and POS - May 30, 2024
- Difference Between RFID and NFC - May 28, 2024
Search DifferenceBetween.net :
3 Comments
Leave a Response
References :
[0]Wallace, Edward C. and Stephen F. West. Roads to Geometry (3rd ed.). Illinois: Waveland Press, 2015. Print
[1]Beckmann, Charlene E., et al. Teaching and Learning High School Mathematics. Hoboken, New Jersey: John Wiley & Sons, 2009. Print
[2]Venema, Gerard. Exploring Advanced Euclidean Geometry with GeoGebra. Washington, D.C.: MAA, 2013. Print
[3]Image credit: https://upload.wikimedia.org/wikipedia/commons/5/55/ASA_Triangle_Congruence.jpg
[4]Image credit: https://upload.wikimedia.org/wikipedia/commons/6/6a/AAS_Triangle_Congruence.jpg

Nice
The AAS is also ASA since having two angles in a triangle you have also the third one.
ASA is not acceptable. It is always AAS.The correct postulate : Two triangles are said be congruent if two angles and one side of one triangle be equal to two angles and the corresponding side of another triangle.