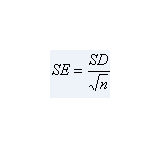Difference between Standard Deviation and Standard Error
Introduction
Standard Deviation (SD) and Standard Error (SE) are seemingly similar terminologies; however, they are conceptually so varied that they are used almost interchangeably in Statistics literature. Both terms are usually preceded by a plus-minus symbol (+/-) which is indicative of the fact that they define a symmetric value or represent a range of values. Invariably, both terms appear with an average (mean) of a set of measured values.
Interestingly, an SE has nothing to do with standards, with errors, or with the communication of scientific data.
A detailed look at the origin and the explanation of SD and SE will reveal, why professional statisticians and those who use it cursorily, both tend to err.
Standard Deviation (SD)
An SD is a descriptive statistic describing the spread of a distribution. As a metric, it is useful when the data are normally distributed. However, it is less useful when data are highly skewed or bimodal because it doesn’t describe very well the shape of the distribution. Typically, we use SD when reporting the characteristics of the sample, because we intend to describe how much the data varies around the mean. Other useful statistics for describing the spread of the data are inter-quartile range, the 25th and 75th percentiles, and the range of the data.
Variance is a descriptive statistic also, and it is defined as the square of the standard deviation. It is not usually reported when describing results, but it is a more mathematically tractable formula (a.k.a. the sum of squared deviations) and plays a role in the computation of statistics.
For example, if we have two statistics P & Q with known variances var(P) & var(Q), then the variance of the sum P+Q is equal to the sum of the variances: var(P) +var(Q). It is now evident why statisticians like to talk about variances.
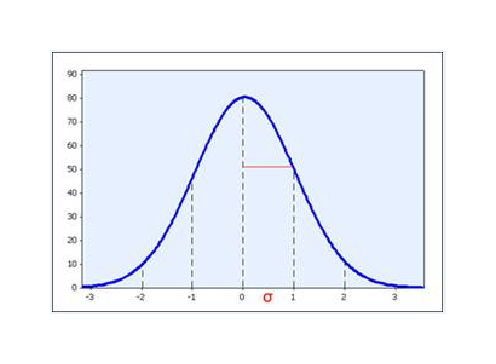
But standard deviations carry an important meaning for spread, particularly when the data are normally distributed: The interval mean +/- 1 SD can be expected to capture 2/3 of the sample, and the interval mean +- 2 SD can be expected to capture 95% of the sample.
SD provides an indication of how far the individual responses to a question vary or “deviate” from the mean. SD tells the researcher how spread out the responses are — are they concentrated around the mean, or scattered far & wide? Did all of your respondents rate your product in the middle of your scale, or did some approve it and some disapprove it?
Consider an experiment where respondents are asked to rate a product on a series of attributes on a 5-point scale. The mean for a group of ten respondents (labeled ‘A’ through ‘J’ below) for “good value for the money” was 3.2 with a SD of 0.4 and the mean for “product reliability” was 3.4 with a SD of 2.1.
At first glance (looking at the means only) it would seem that reliability was rated higher than value. But the higher SD for reliability could indicate (as shown in the distribution below) that responses were very polarized, where most respondents had no reliability issues (rated the attribute a “5”), but a smaller, but important segment of respondents, had a reliability problem and rated the attribute “1”. Looking at the mean alone tells only part of the story, however, more often than not, this is what researchers focus on. The distribution of responses is important to consider and the SD provides a valuable descriptive measure of this.
| Respondent | Good Value for the Money | Product Reliability |
| A | 3 | 1 |
| B | 3 | 1 |
| C | 3 | 1 |
| D | 3 | 1 |
| E | 4 | 5 |
| F | 4 | 5 |
| G | 3 | 5 |
| H | 3 | 5 |
| I | 3 | 5 |
| J | 3 | 5 |
| Mean | 3.2 | 3.4 |
| Std. Dev. | 0.4 | 2.1 |
First Survey: Respondents rating a product on a 5-point scale
Two very different distributions of responses to a 5-point rating scale can yield the same mean. Consider the following example showing response values for two different ratings.
In the first example (Rating “A”), SD is zero because ALL responses were exactly the mean value. The individual responses did not deviate at all from the mean.
In Rating “B”, even though the group mean is the same (3.0) as the first distribution, the Standard Deviation is higher. The Standard Deviation of 1.15 shows that the individual responses, on average*, were a little over 1 point away from the mean.
| Respondent | Rating “A” | Rating “B” |
| A | 3 | 1 |
| B | 3 | 2 |
| C | 3 | 2 |
| D | 3 | 3 |
| E | 3 | 3 |
| F | 3 | 3 |
| G | 3 | 3 |
| H | 3 | 4 |
| I | 3 | 4 |
| J | 3 | 5 |
| Mean | 3.0 | 3.0 |
| Std. Dev. | 0.00 | 1.15 |
Second Survey: Respondents rating a product on a 5-point scale
Another way of looking at SD is by plotting the distribution as a histogram of responses. A distribution with a low SD would display as a tall narrow shape, while a large SD would be indicated by a wider shape.
SD generally does not indicate “right or wrong” or “better or worse” — a lower SD is not necessarily more desirable. It is used purely as a descriptive statistic. It describes the distribution in relation to the mean.
Technical disclaimer relating to SD
Thinking of SD as an “average deviation” is an excellent way of conceptually understanding its meaning. However, it is not actually calculated as an average (if it were, we would call it the “average deviation”). Instead, it is “standardized,” a somewhat complex method of computing the value using the sum of the squares.
For practical purposes, the computation is not important. Most tabulation programs, spreadsheets or other data management tools will calculate the SD for you. More important is to understand what the statistics convey.
Standard Error
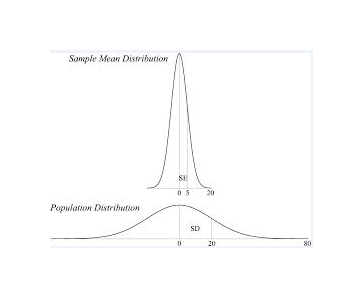
A standard error is an inferential statistic that is used when comparing sample means (averages) across populations. It is a measure of precision of the sample mean. The sample mean is a statistic derived from data that has an underlying distribution. We can’t visualize it in the same way as the data, since we have performed a single experiment and have only a single value. Statistical theory tells us that the sample mean (for a large “enough” sample and under a few regularity conditions) is approximately normally distributed. The standard deviation of this normal distribution is what we call the standard error.
When we want to compare the means of outcomes from a two-sample experiment of Treatment A vs. Treatment B, then we need to estimate how precisely we’ve measured the means.
Actually, we are interested in how precisely we’ve measured the difference between the two means. We call this measure the standard error of the difference. You may not be surprised to learn that the standard error of the difference in the sample means is a function of the standard errors of the means:
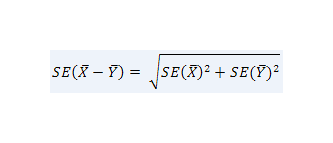
,where n is the number of data points.
Notice that the standard error depends upon two components: the standard deviation of the sample, and the size of the sample n. This makes intuitive sense: the larger the standard deviation of the sample, the less precise we can be about our estimate of the true mean.
Also, the large the sample size, the more information we have about the population and the more precisely we can estimate the true mean.
SE is an indication of the reliability of the mean. A small SE is an indication that the sample mean is a more accurate reflection of the actual population mean. A larger sample size will normally result in a smaller SE (while SD is not directly affected by sample size).
Most survey research involves drawing a sample from a population. We then make inferences about the population from the results obtained from that sample. If a second sample was drawn, the results probably won’t exactly match the first sample. If the mean value for a rating attribute was 3.2 for one sample, it might be 3.4 for a second sample of the same size. If we were to draw an infinite number of samples (of equal size) from our population, we could display the observed means as a distribution. We could then calculate an average of all of our sample means. This mean would equal the true population mean. We can also calculate the SD of the distribution of sample means. The SD of this distribution of sample means is the SE of each individual sample mean.
We, thus, have our most significant observation: SE is the SD of the population mean.
| Sample | Mean |
| 1st | 3.2 |
| 2nd | 3.4 |
| 3rd | 3.3 |
| 4th | 3.2 |
| 5th | 3.1 |
| …. | …. |
| …. | …. |
| …. | …. |
| …. | …. |
| …. | …. |
| Mean | 3.3 |
| Std. Dev. | 0.13 |
Table illustrating the relation between SD and SE
It is now clear that if the SD of this distribution helps us to understand how far a sample mean is from the true population mean, then we can use this to understand how accurate any individual sample mean is in relation to the true mean. That is the essence of SE.
In actuality, we have only drawn a single sample from our population, but we can use this result to provide an estimate of the reliability of our observed sample mean.
In fact, SE tells us that we can be 95% confident that our observed sample mean is plus or minus roughly 2 (actually 1.96) Standard Errors from the population mean.
The below table shows the distribution of responses from our first (and only) sample used for our research. The SE of 0.13, being relatively small, gives us an indication that our mean is relatively close to the true mean of our overall population. The margin of error (at 95% confidence) for our mean is (roughly) twice that value (+/- 0.26), telling us that the true mean is most likely between 2.94 and 3.46.
| Respondent | Rating |
| A | 3 |
| B | 3 |
| C | 3 |
| D | 3 |
| E | 4 |
| F | 4 |
| G | 3 |
| H | 3 |
| I | 3 |
| J | 3 |
| Mean | 3.2 |
| Std. Err | 0.13 |
Summary
Many researchers fail to understand the distinction between Standard Deviation and Standard Error, even though they are commonly included in data analysis. While the actual calculations for Standard Deviation and Standard Error look very similar, they represent two very different, but complementary, measures. SD tells us about the shape of our distribution, how close the individual data values are from the mean value. SE tells us how close our sample mean is to the true mean of the overall population. Together, they help to provide a more complete picture than the mean alone can tell us.
- Difference between Wibree and Bluetooth - February 17, 2016
- Difference between Standard Deviation and Standard Error - February 3, 2016
- Difference between Tethering and Hotspot - January 11, 2016