Difference Between Quick Sort and Merge Sort

Sorting items in a list is a mundane task and often time consuming. The term sorting generally refers to arranging the items in a list in either ascending or descending order based on a pre-specified ordering relation. Sorting is often intended for searching, which his yet another fundamental activity in data processing. Imagine how difficult it would have been to search a word on a dictionary if the words in it hadn’t been organized or sorted. This is the reason why entries in a dictionary are kept in a standard alphabetic order. Numerous tasks and computations become effortless simply by sorting. And this is where sorting algorithms come to the picture.

A sorting algorithm is nothing but a method to organize elements of a list into a specific order, such as lowest-to-highest value, highest-to-lowest value, increasing order, decreasing order, alphabetical, etc. The most commonly used orders are numerical and lexicographical order. Algorithms often use sorting as a key subroutine. There are a wide variety of sorting algorithms used throughout, each employing a rich set of techniques. One such popular yet equally powerful algorithm is Divide and Conquer algorithm which is an algorithm based on multi-branched recursion. Quick Sort and Merge Sort are the two commonly used algorithms based on Divide and Conquer algorithm.

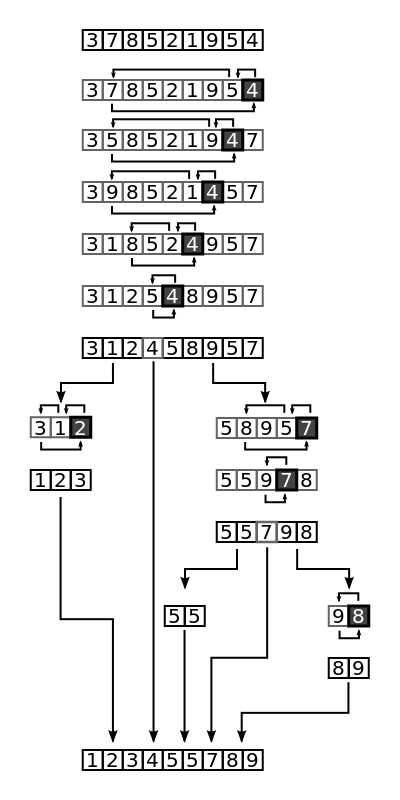
What is Quick Sort?

Quick Sort is a highly efficient yet effective sorting algorithm based on the divide and conquer approach which is quite similar to the dynamic approach in which a problem is divided into two or more sub-problems and then solved recursively. If the size of the sub-problems is small enough, then they are solved simply in a straightforward manner without any hassles. Also called partition-exchange sort, the quick sort algorithm divides the list to be sorted into three main parts: 1) Pivot element (central elements), 2) elements less than the pivot, and 3) elements greater than the pivot. The pivot itself is moved between the two groups to its final position and QUICK SORT is then applied recursively.

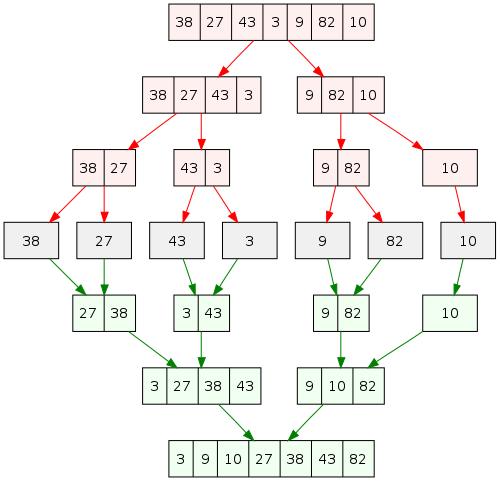
What is Merge Sort?

Merge Sort is yet another general-purpose sorting algorithm based on the divide and conquer technique. It is one of the most respected and popular sorting algorithms designed to be used efficiently to sort data that is stored externally in a file. It offers O (n log n) behavior in the worst case while using O (n) extra storage. It divides a collection ‘A’ into two smaller collections, each of which is then sorted. In the final phase, these two sorted collections are merged back into a single collection of size n. This will be the sorted list. The algorithm is quite fast and is also a stable sort, and is ideally preferred for Linked Lists.

Difference between Quick Sort and Merge Sort

Basics

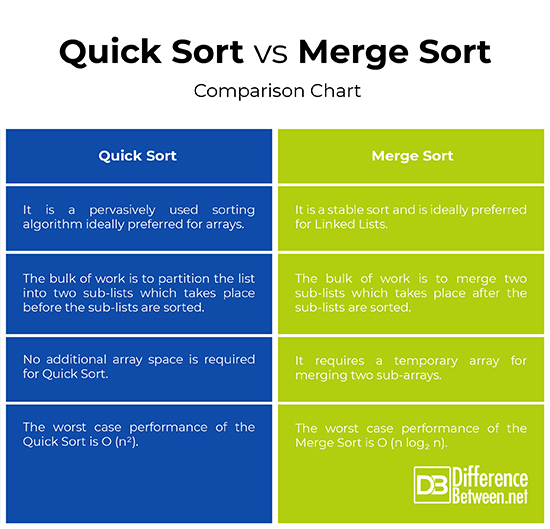
– Both Quick Sort and Merge Sort are the divide-and-conquer-based sorting algorithms with the same basic principle – to divide a problem into two or more sub-problems and then solve them recursively. However, they differ in the merge procedures and in terms of performance. Quick Sort is generally better and faster than other sorting algorithms including Merge Sort when it comes to small data set, whereas Merge Sort maintains consistency regardless of the type of data sets. Quick Sort is ideally preferred for arrays whereas Merge Sort is ideally preferred for Linked Lists.

Space Complexity

– The sorting in Quick Sort algorithm is done recursively, and each recursive call requires stack place. It does not require extra space for merging, except a single memory space for merging. As it is an in-place sorting algorithm, no additional space is required to perform sorting. In fact, it uses the same array while dividing and merging the array. In Merge Sort, on the other hand, there are several ways of representing data in a file or as an array, so it needs such work areas as sub-files or arrays of the same size which require extra space.

Worst Case Complexity

– The worst case behavior for Quick Sort occurs when the partitioning is unbalanced which depends on which elements are used for partitioning, in which case, the algorithm runs asymptotically as slowly as insertion sort. The worst case performance of the Quick Sort is O (n²) and is left as an exercise. However, it can be avoided by choosing the right pivot. The worst case of Merge Sort, on the other hand, occurs when it has to do maximum number of comparisons. Considering the linear performance for merging, the worst case performance of the Merge Sort is O (n log₂ n).

Performance

– Although both Quick Sort and Merge Sort algorithms are based on the divide and conquer approach for sorting, they differ by the methods used to perform the split and the merge procedures. For Quick Sort, the bulk of work is to partition the list into two sub-lists which takes place before the sub-lists are sorted. For Merge Sort, the bulk of work is to merge two sub-lists which takes place after the sub-lists are sorted. Merge Sort requires a temporary array for merging two sub-arrays, whereas no additional array space is required for Quick Sort, making it more space efficient than Marge Sort.

Quick Sort vs. Merge Sort: Comparison Chart

Summary of Quick Sort vs. Merge Sort

Both Quick Sort and Merge Sort algorithms are based on the divide and conquer approach for sorting. However, they differ by the methods used to perform the split and the merge procedures. They basically work on the same principle – to divide a problem into two or more sub-problems and then solve them recursively. Merge Sort is more efficient than Quick Sort in the worst case, but the two are equally efficient in the average case. But Quick Sort is more space efficient than Merge Sort. So Quick Sort is undoubtedly faster and better than Merge Sort but it becomes inefficient in few situations such as when it comes to comparisons.

Sharing is caring!