Difference Between Definite and Indefinite Integrals
Calculus is an important branch of mathematics, and differentiation plays a critical role in calculus. The inverse process of the differentiation is known as integration, and the inverse is known as the integral, or simply put, the inverse of differentiation gives an integral. Based on the results they produce the integrals are divided into two classes viz., definite and indefinite integrals.
Definite Integral
The definite integral of f(x) is a NUMBER and represents the area under the curve f(x) from x=a to x=b.
A definite integral has upper and lower limits on the integrals, and it’s called definite because, at the end of the problem, we have a number – it is a definite answer.
Indefinite Integral
The indefinite integral of f(x) is a FUNCTION and answers the question, “What function when differentiated gives f(x)?”
With an indefinite integral there are no upper and lower limits on the integral here, and what we’ll get is an answer that still has x‘s in it and will also have a constant (usually denoted by C) in it.
Indefinite integral usually gives a general solution to the differential equation.
Indefinite integral is more of a general form of integration, and it can be interpreted as the anti-derivative of the considered function.
Suppose differentiation of function F leads to another function f, and the integration of f gives the integral. Symbolically, this is written as
F(x)=∫ƒ(x)dx
or
F=∫ƒ dx
where both F and ƒ are functions of x, and F is differentiable. In the above form, it is called a Reimann integral and the resulting function accompanies an arbitrary constant.
An indefinite integral often produces a family of functions; therefore, the integral is indefinite.
Integrals and integration process are at the heart of solving differential equations. However, unlike the steps in differentiation, steps in integration do not always follow a clear and standard routine. Occasionally, we see that the solution cannot be expressed explicitly in terms of elementary function. In that case, the analytic solution is often given in the form of an indefinite integral.
Fundamental Theorem of Calculus
The definite and the indefinite integral are linked by the Fundamental Theorem of Calculus as follows: In order to compute a definite integral, find the indefinite integral (also known as the anti-derivative) of the function and evaluate at the endpoints x=a and x=b.
The difference between definite and indefinite integrals will be evident once we evaluate the integrals for the same function.
Consider the following integral:
OK. Let’s do both of them and see the difference.
For integration, we need to add one to the index which leads us to the following expression:
At this point of time C is merely a constant to us. Additional information is needed in the problem to determine the precise value of C.
Let us evaluate the same integral in its definite form i.e., with the upper and lower limits included.
Graphically speaking, we are now computing the area under the curve f(x) = y3 between y=2 and y=3.
The first step in this evaluation is the same as the indefinite integral evaluation. The only difference is that this time around we do not add the constant C.
The expression in this case looks as follows:
This is turn leads to:
Essentially, we substituted 3 and then 2 in the expression and obtained the difference between them.
This is the definite value as opposed to the usage of constant C earlier.
Let’s explore the constant factor (with regard to indefinite integral) in some more detail.
If the differential of y3 is 3y2, then
∫3y2dy = y3
However, 3y2 could be the differential of many expressions some of which include y3-5, y3+7, etc.. This implies that the reversal is not unique since the constant is unaccounted for during the operation.
So in general, 3y2 is the differential of y3+C where C is any constant. Incidentally, C is known as the ‘constant of integration’.
We write this as:
∫ 3y2.dx = y3 + C
Integration techniques for an indefinite integral, such as table lookup or Risch integration, can add new discontinuities during the integration process. These new discontinuities appear because the anti-derivatives can require the introduction of complex logarithms.
Complex logarithms have a jump discontinuity when the argument crosses the negative real axis, and the integration algorithms sometimes cannot find a representation where these jumps cancel.
If the definite integral is evaluated by first computing an indefinite integral and then substituting the integration boundaries into the result, we must be aware that indefinite integration might produce discontinuities. If it does, additionally, we must investigate the discontinuities in the integration interval.
- Difference between Wibree and Bluetooth - February 17, 2016
- Difference between Standard Deviation and Standard Error - February 3, 2016
- Difference between Tethering and Hotspot - January 11, 2016

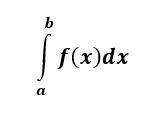
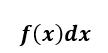
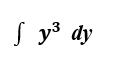
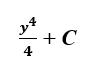
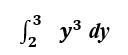
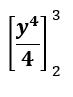
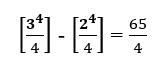
Thanks