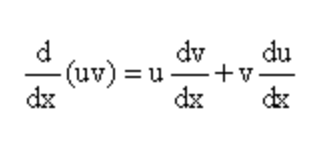Difference Between Differentiation and Integration 

Calculus is one of the primary mathematical applications that are applied in the world today to solve various phenomenon. It is highly employed in scientific studies, economic studies, finance, and engineering among other disciplines that play a vital role in the life of an individual. Integration and differentiation are the fundamentals used in calculus to study change. However, many people, including students and scholars have not been able to highlight differences between differentiation and integration.

What is Differentiation?

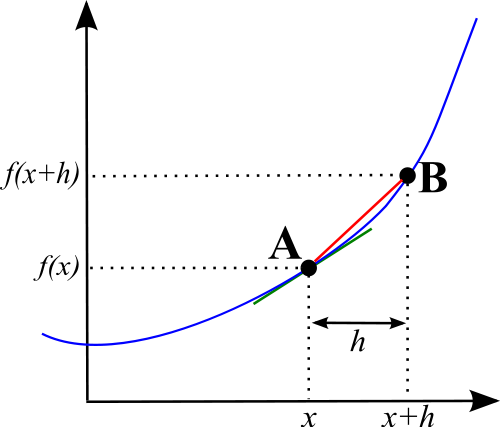
Differentiation is a term used in calculus to refer to the change in, which properties experiences concerning a unit change in another related property.

In another term, differentiation forms an algebraic expression that helps in the calculation the gradient of a curve at given point. It is important to highlight that curves have their slopes varying at given point unlike straight lines, which have the same gradient all through.

What is Integration?

Integration is a term used in calculus to refer to the formula and the procedure of calculating the area under the curve.

It is worth noting that the graph must be under a curve, which results to the formation of an integral part, which is difficult to find the area unlike other shapes like circles, squares, and rectangles, which are easier to calculate their areas.

Difference Between Differentiation and Integration

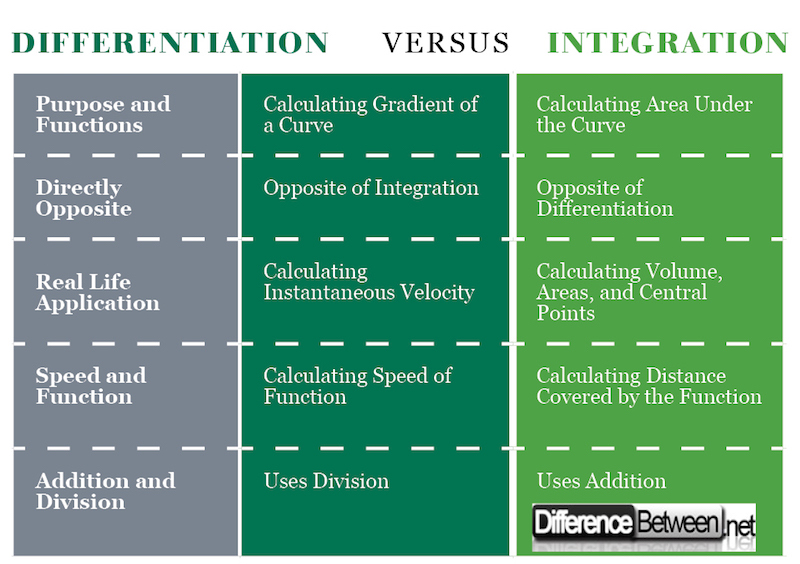
1) Purpose and Functions of Differentiation and Integration

Integration and differentiation can be primarily be differentiated in the way the two concepts are applied and their ultimate results. They are used to arrive at different answers, which is the fundamental difference. Differentiation is used in calculating the gradient of the curve. Nonlinear curves have different slopes at any given point, which makes it difficult to determine their gradients. The algebraic expression used to determine the change incurred from one point to another with a unit is referred to as differentiation.  On the other hand, integration is an algebraic expression used in calculating the area under the curve because it is not a perfect shape after which area can easily be calculated.

2) Directly Opposite

Differentiation and Integration algebraic functions are directly opposite of one another, specifically in their application. If one performs integration, he or she is said to be showing the opposite of differentiation while if one performs differentiation, he or she is performing opposite of integration. For example, integration and differentiation form a relationship that is similarly depicted when one performs the square of a number and then finds the square root of the result. Therefore, if one wants to find the opposite of an integrated number, he or she will be required to perform the differentiation of the same number. Simply, integration is the reverse process of differentiation and vice versa.

3) Real Life Application for Differentiation and Integration

In real life scenarios, integration and differentiation have been found to be applied differently to each concept used in providing different results. Nevertheless, it is remarkable to highlight that both differentiation is essential calculus concepts that make life easy. One of the main application of integration is calculating the areas of curved surfaces, calculating the volume of objects, and calculating the central point among other functions.

On the other hand, differentiation concept is significantly used in calculating instantaneous velocity and used in determining whether a function is increasing or decreasing accordingly. This is a clear demonstration of how the two concepts are applied in the lives of individuals.

4) Speed and Function of Differentiation and Integration

The other difference between integration and differentiation is the role they play when it comes to any given function under investigation. According to mathematicians, differentiation significantly helps in determining the speed of the function by helping in the calculation of instantaneous velocity. On the other hand, integration is concerned with determining the distanced travelled by any given function. The area under the curve is estimated to be equivalent to the distance travelled by the function. Integration algebraic expression helps in calculating the area under the curve, which amounts to the distance travelled by the function.

Algebraic Expressions/Formula for Differentiation and Integration

It is also worth noting that differentiation and integration have different algebraic expressions, which are used in the calculation. This explains why the two calculus concepts will always provide different results.  The derivative of a function f(x) concerning the variable x and according to the product rule will be defined as:

On the other hand, the integration formula or the integral area under the curve can be calculated by use of the formula:

∫f(x) dx, which is the formula adopted under substitution method.

5) Addition and Division

The other method of comparing integration to differentiation is by specifically explaining how each function realizes its results. Integration determines the outcome of a specific function by adding the aspects associated with calculation. On the other hand, differentiation determines instantaneous velocity and the speed of the function through division.

Differences Between Differentiation and Integration: Comparison Chart

Summary of Differentiation vs. Integration

• One of the principal variations between differentiation and integration is that the two calculus functions are directly opposite of one another in their application.
• Students and other scholars should focus on understanding one of the concepts after which they will be required to perform the opposite to determine the results of the other function.
• Understanding differences that exist between integration and differentiation are essential because it will help individuals to use the right algebraic expression where necessary.
• Lastly, it is vital to master the two calculus concepts in basic mathematics because they have consistently been used in various disciplines like economics, business, and engineering.

Sharing is caring!