Difference Between Exponential Growth and Exponential Decay

Exponential growth is exponentially increasing values with time while decay is exponentially decreasing values with time.

What is Exponential Growth?

Definition of Exponential growth:

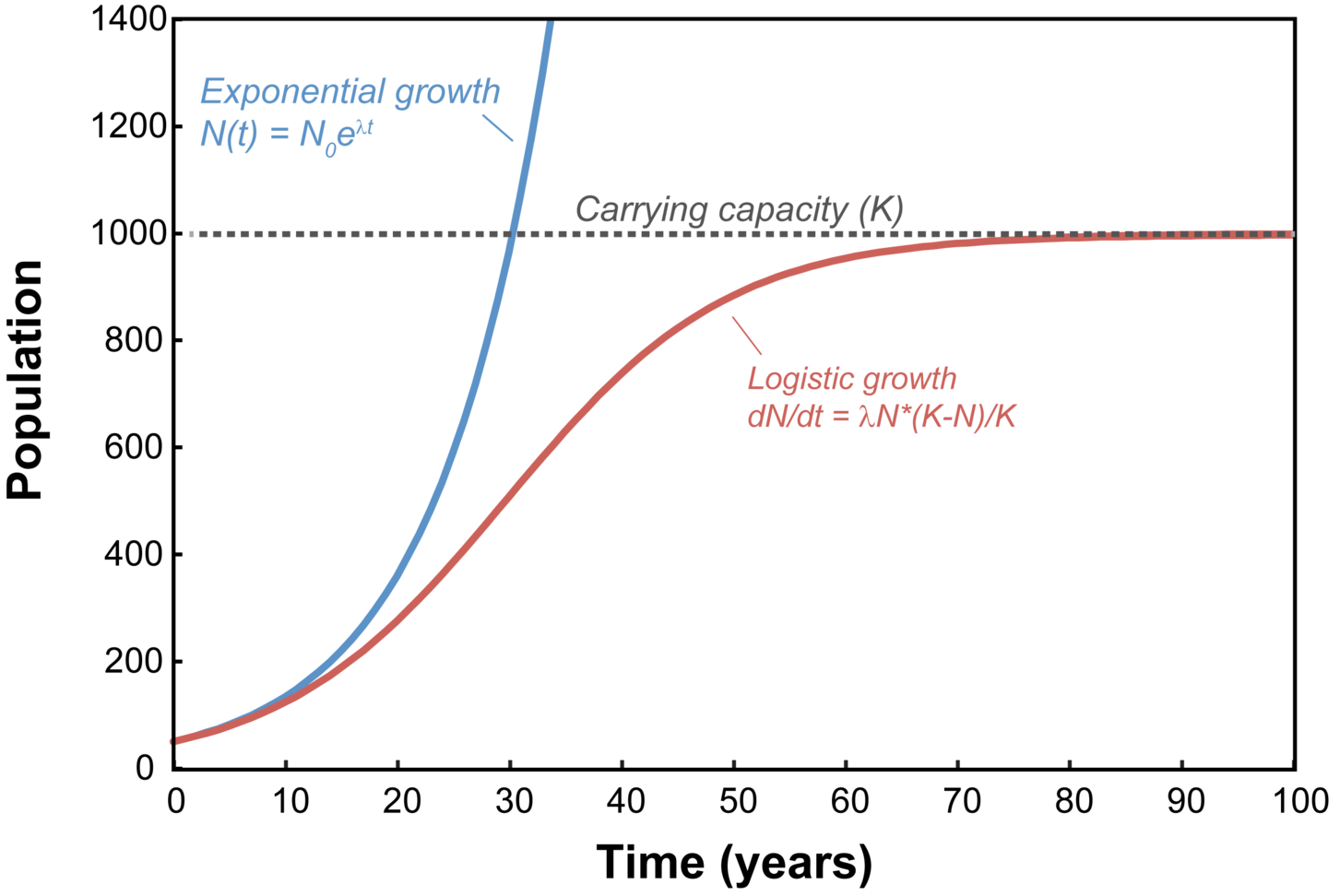
Exponential growth is when the number of some entity increases rapidly in an exponential manner over time. An exponential growth mathematical function is one in which numbers multiply in size as time progresses. An exponent is part of the equation as well, so for instance, an equation could be y = 5*2^x.  In this case, each number, starting at 5 is multiplied by 2 to an exponent power such as 2. The exponent is usually an integer greater than 1, such that when a number is raised to this power, it produces an even larger number.

Graph for Exponential growth:

Drawing a graph of this function would produce a curved line that goes upwards. The slope would be constantly changing as more numbers are put into the equation. To get an equation for the slope you would have to calculate the derivative using calculus. As the numbers on the x-axis of the graph, the time variable, become bigger so do the numbers on the y-axis, the size variable. The relationship between the variables is not an inverse one and slopes upwards.

Exponential growth  Examples:

Examples of exponential growth can be seen in populations of bacteria which divide very rapidly. Salmonella enterica serovar Typhimurium bacteria, for instance, have been extensively studied and shown to have a lag phase during which time they prepare to enter a pattern of exponential growth. The bacteria will divide and the population will grow exponentially until there are no more nutrients left.

Uses of Exponential growth:

Knowing the growth rate of bacteria under various conditions can be useful in enabling scientists to develop various antimicrobial agents. These antibiotics can then be tested and evaluated based on their impact on the exponential growth rate of the bacterial target.

What is Exponential Decay?

Definition of Decay:

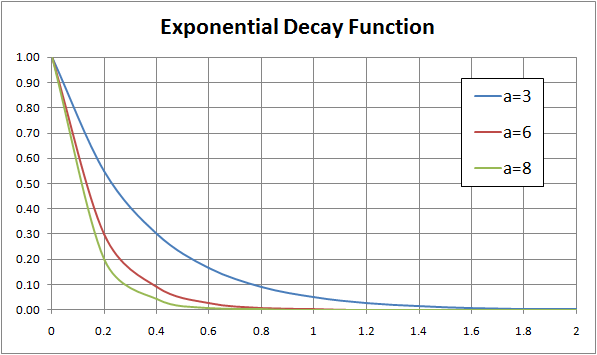
Decay is when numbers decrease over time in an exponential fashion, thus the result looks something like a repeated division. An exponential equation is still involved but the exponent is such that the values keep decreasing or decaying over time. For example, let’s say we have an equation:  y = 5*2^x.  In this case, each number, starting at 5 is multiplied by 2 to an exponent power such as 1/2. The exponent is a fraction such that the numbers decrease in size when plugged into the equation.

Graph:

Drawing a graph of this function would produce a curved line that goes downwards. The slope would be constantly changing as more numbers are put into the equation. To get an equation for the slope you would have to calculate the derivative using calculus. As the numbers on the x-axis of the graph, the time variable, become bigger so the numbers on the y-axis, the size variable become smaller. This is an inverse relationship between the two variables of time and size, and the graph slopes downwards.

Examples of Exponential Decay:

A good example of decay is the value of a new car. When you first buy the car it is worth a lot of money, but as time goes on it depreciates and loses value so that if you were to sell the car you would get less for it than you paid in the beginning. In science, the radioactive decay of isotopes is a good example of a natural process of decay which occurs. The half-life of an isotope is the time it takes for half of the atom to decay.

Uses:

Knowing the radioactive decay of certain isotopes has been very useful as it has enabled scientists to date fossils that have been found in sedimentary rock layers. This gives an indication of what life was present on earth during each geological time period.

Difference between Exponential Growth and Exponential Decay

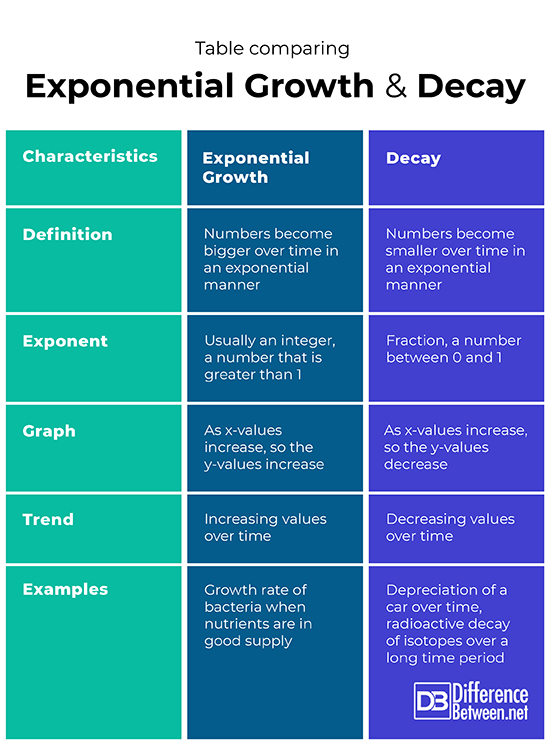
Definition

In exponential growth, numbers increase in value over time in an exponential fashion. In decay, numbers decrease in value over time in an exponential fashion.

Exponent

The exponent in the equation in the case of exponential growth is usually an integer, a number that is greater than 1. The exponent in the equation for decay is a fraction that is between 0 and 1.

Graph

In the case of exponential growth, the y-values on a graph will increase as the x-values increase. In the situation of decay, the y-values on the graph will decrease as the x-values increase.

Trend

The trend that is evident in exponential growth is increasingly large numbers over time. The trend in decay is the reverse of that seen with exponential growth and instead, it is increasingly small numbers over time.

Examples

Exponential growth rate examples include the growth rates of several types of bacteria when conditions are optimal and before the substrate is depleted. Decay examples include the decreasing value of a car (depreciation) over time and the radioactive decay of radioactive isotopes with time.

Table comparing Exponential growth and Decay

Summary of Exponential growth Vs. Decay

• Both exponential growth and decay can be described mathematically using equations involving an exponent.
• Both exponential growth and decay involve a rapid change in numbers.
• The exponent for exponential growth is always positive and greater than 1.
• The exponent for decay is always between 0 and 1.
• Exponential growth is when numbers increase rapidly in an exponential fashion so for every x-value on a graph there is a larger y-value.
• Decay is when numbers decrease rapidly in an exponential fashion so for every x-value on a graph there is a smaller y-value.
• An example of exponential growth is the rapid population growth rate of bacteria.
• An example of decay is the depreciation of the value of a car, and the radioactive decay of isotopes.

Sharing is caring!