Difference Between Power and Exponent

Powers and exponents are tools to rewrite long multiplication problems in mathematics, especially algebra.

Algebra is one of the key branches of mathematics that deals primarily with the number theory. It is also referred to as the study of mathematical symbols. You might have noticed superscript in mathematical relationships, the one that is placed above to the right of a number. This is called an exponent and the whole expression is called as exponentiation.

The operation involves two numbers written as x^a, where ‘x’ is the base number and ‘a’ is the exponent. The exponent is basically a superscript used to simplify larger mathematical problems. The whole expression is called “power” and written as “x to the power of a” where ‘a’ is a positive integer.

What is Power in Mathematics?

Power is a mathematical expression used to represent exactly how many times a number should be used in a multiplication. In simple terms, it is an expression that describes repeated multiplication of the same number. The expression can be written as “raising a number to the power”. Consider the following example: 3 x 3 x 3 x 3 = 81. This can also be written as 3⁴ = 81. This is an exponential notation which simply means the number the number ‘3’ is multiplied four times by itself to get 27 or we can say “3 raised to the power of 4” or “3 raised to the 4^th power” is 27. The number ‘3’ is the base number and ‘4’ is called the power or exponent.

What is Exponent?

Exponent is often used interchangeably with power but in a different context. While power represents the whole expression, exponent is the superscript placed above to the right of the base number. It is a positive or negative number which represents the power to which the base number is raised meaning it states the number of times a number is to be used in a multiplication. In 5³ = 5 x 5 x 5 = 125, the base number ‘5’ is used thrice in a multiplication meaning we are multiplying 5 three times by itself. Exponents often go by powers or indices. The two most commonly used exponents in geometry are square and cube. For example, ‘a²’ is ‘a square’ and ‘a³’ is ‘a cube’. If the exponent is 1, then the result is the base number and if the exponent is 0, then the result is always 1. For example, 2¹ = 2 and 2⁰ = 1.

Difference between Power and Exponent

Definition of Power and Exponent

In mathematical relationships, power refers to the number of times a number is multiplied by itself meaning the number you get raising a number to an exponent whereas an exponent is the number of times the number is used in a multiplication. Exponents are often called powers or indices. In simple terms, power is an expression that represents repeated multiplication of the same number whereas exponent is refers to a quantity that represents the power to which the number is raised. Both terms are often used interchangeably in mathematical operations.

Representation of Power and Exponent

Hypothetically, the terms power and exponent are synonymous but they are used in different contexts in mathematics. It’s a number placed above or after another number to represent the power to which the latter is to be raised. Let’s say, when we write “a^b” – ‘a’ is the base, ‘b’ is the exponent, and the whole thing represents “a to the power of b”. Here, the phrase “to the power of b” means ‘b’ is the power which is often used interchangeably with exponent. Rather, ‘b’ identifies the power you are referring to in the relation. Basically, power is used to represent two things, base number and the exponent.

Example of Power and Exponent

The expression 5 x 5 x 5 can be written in a shorter way as 5³ using exponents.

5 x 5 x 5 = 5³

The expression represents repeated multiplication of the same number called a power. Here’ the number ‘5’ represents the base and the number ‘3’ represents the exponent and the whole expression says “5 to the power of 3” or “5 to the third power” meaning 5 is multiplied by itself three times.

Similarly, 2⁵ = 2 x 2 x 2 x 2 x 2 = 16

The expression can be called “2 to the power of 5” or “2 to the 5^th power”. Exponents make it easy to write and use multiplications factor in mathematics.

Power vs. Exponent: Comparison Chart

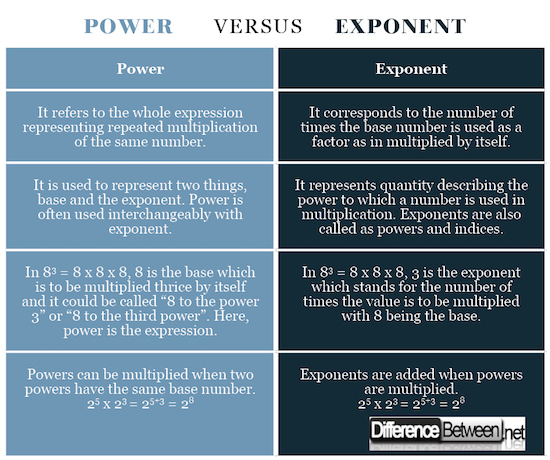
Summary of Power vs Exponent

Power and exponent both are very important tools in mathematics used to represent repeated multiplications. An exponent is nothing but a number or a variable that represents the number of times the base number is multiplied by itself. In the mathematical expression 2⁴, 2 is the base number with an exponent of 4 meaning 4 is the superscript of 2 and the form is called exponential form. Power is synonymous with exponent, but is used in a different context. Power refers to the whole expression of writing the exponent to the head of the base number. In 2³, 2 is the base and 3 is the exponent and the expression says 2 to the power of 3 or 2 to the third power.

Sharing is caring!