Differences between Correlation and Regression

Both Correlation and Regression are statistical tools that deal with two or more variables. Although both relate to the same subject matter, there are differences between the two. The differences, between the two are explained below.

Meaning

The term correlation with reference to two or more variables signifies that the variables are related in some way. Correlation analysis determines whether a relationship between two variables exists, and the strength of the relationship. If two variables x (independent) and y (dependent) are so related that variation in the magnitude of independent variable is accompanied, by variation in magnitude of dependent variable then the two variables are said to be correlated.

Correlation can be linear or non-linear. A linear correlation is one where the variables are so related that change in the value of one variable would cause a change in the value of other variable consistently. In a linear correlation the scattered points related to the respective values of dependent and independent variables would cluster around a non-horizontal straight line, although a horizontal straight line would also indicate a linear relationship between the variables if a straight line could connect the points representing the variables.

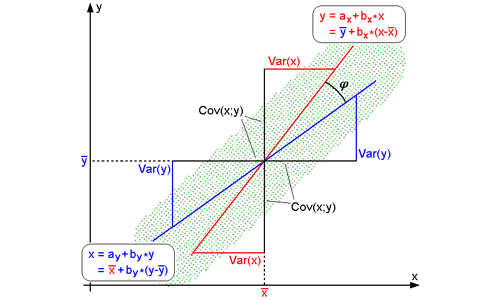
Regression analysis, on the other hand, uses the existing data to determine a mathematical relationship between the variables which can be used to determine the value of the dependent variable with respect to any value of the independent variable.

Statistical orientation

Correlation is concerned with the measurement of strength of association or intensity of relationship, where as regression is concerned with prediction of the value of dependent variable in relation to a known value of the independent variable. This can be explained with the following formulae.

Correlation coefficient or coefficient correlation (r) between x & y is found out with the following formula;

r = covariance(x,y)/σx.σy, cov(x,y) = Σxy/n – (Σx/n)(Σy/n), σx  & σy are standard deviations of x and y respectively, and, -1 < r < +1. The correlation coefficient r is independent of choice of both origin and scale of observation. Thud if u = (x-c)/d, and, v = (y-c′)/d′, where c, c′, d, d′ are arbitrary constant, and d, d′ > 0, then correlation coefficient between x and y = correlation coefficient between u and v.

Correlation coefficient r is a pure number and independent of unit of measurement. Thus if x is height (inches) and y is weight (lbs.) of people of a certain region, then r is neither in inches nor in lbs., but simply a number.

Regression equation is found out with the following formula;

Regression equation of y on x (to find out estimate of y) is y – y′ = byx(x-x‾), byx is called Regression coefficient of y on x. Regression equation of x on y (to find out estimate of x) is x – x′ = bxy(y-y‾), bxy is called Regression coefficient of x on y.

Correlation analysis does not assume dependence of any variable on other variable, neither does it tries to find out the relationship between the two. It simply estimates the degree of association between variables. In other words correlation analysis tests interdependence of variables. Regression analysis on the other hand describes the dependence of the dependent variable or response variable on the independent or explanatory variable/s. Regression analysis assumes that there exists a one-way causal relationship between explanatory and response variables, and does not take into account whether that causal relationship is positive or negative. For correlation both the values of dependent and independent variables are random, but for regression values of independent variables need not be random.

Summary

1. Correlation analysis is a test of inter-dependence between two variables. Regression analysis gives a mathematical formula to determine value of the dependent variable with respect to a value of independent variable/s.

2. Correlation coefficient is independent of choice of origin and scale, but regression coefficient is not so.

For correlation the values of both the variables have to be random, but this is not so for regression coefficient.

Bibliography

1. Das, N. G., (1998), Statistical Methods, Calcutta

2. Correlation & Regression, available at www.le.ac.uk/bl/gat/virtualfc/stats/regression

3. Regression & Correlation, available at www.abyss.uoregon.edu

Sharing is caring!