Parabola vs Hyperbola
Parabola and hyperbola are two different sections of a cone. We can deal with their differences in a mathematical explanation or deal with the differences in a very simple way which not only mathematicians but everybody can understand. This article will try to explain the difference between them in a very simple way.
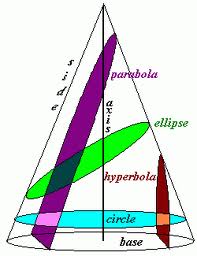
First of all, when a solid figure, which in this case is a cone, is cut by a plane, the section which is obtained is called a conic section. Conic sections could be circles, ellipses, hyperbolas, and parabolas depending upon the angle of intersection between axis of the cone and the plane. Both parabolas and hyperbolas are an open curve which means that the arms or branches of the curves continue to infinity; they are not closed curves like a circle or an ellipse.
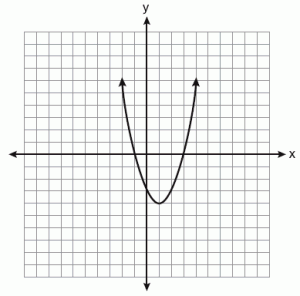
Parabola
A parabola is the curve obtained when the plane cuts parallel to the cone side. In a parabola, a line passing through the focus and perpendicular to the directrix is called an “axis of symmetry.” When the parabola is intersected by the point on the “axis of symmetry,” it is referred to as the “vertex.” All parabolas are shaped identically as they are cut at a specific angle. It is a characterized by the eccentricity of “1.” This is the reason why they are all the same shape but can be of different sizes.
The parabola is given by the equation y2=X
When a set of points present in a plane are equidistant from the directrix, a given straight line, and are equidistant from the focus, a given point which is fixed, it is called a parabola.
Parabolas have many practical applications. They are used for designing the path of missiles, headlight reflectors of automobiles, telescopes, radar receivers, and satellite dishes.
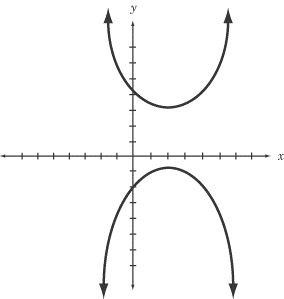
Hyperbola
Hyperbola is the curve obtained when the plane cuts almost parallel to the axis. Hyperbolas are not identical in shape as there are many angles between the axis and the plane. “Vertices” are the points on the two arms which are closest; whereas the line segment which connects the arms is called the “major axis.”
In a parabola, the two arms of the curve, also called branches, become parallel to each other. In a hyperbola, the two arms or curves do not become parallel. A hyperbola’s center is the midpoint of the major axis.
Hyperbola is given by the equation XY=1
When the difference of distances between a set of points present in a plane to two fixed foci or points is a positive constant, it is called a hyperbola.
Summary:
When a set of points present in a plane are equidistant from the directrix, a given straight line, and are equidistant from the focus, a given point which is fixed, it is called a parabola. When the difference of distances between a set of points present in a plane to two fixed foci or points is a positive constant, it is called a hyperbola.
All parabolas are of the same shape no matter what the size; all hyperbolas are of different shapes
The parabola is given by the equation y2=X; a hyperbola is given by the equation XY=1
In a parabola the two arms become parallel to each other whereas in a hyperbola they do not.
- Difference Between Data Mining and Data Warehousing - October 21, 2012
- Difference Between 7-Keto DHEA and DHEA - October 20, 2012
- Difference Between Tamil and Malayalam - October 18, 2012

I’d like this website & many think are clear from this web!
Thanks!
Reply
Wow great job guyz this help me a lot will ace this math test
Reply
“a very simple way which not only mathematicians but everybody can understand”…
…”In a parabola, a line passing through the focus and perpendicular to the directrix is called an “axis of symmetry.”
Hmmm…
Reply
❖
Reply
“When a set of points present in a plane are equidistant from the directrix, a given straight line, and are equidistant from the focus, a given point which is fixed, it is called a parabola.”
Phew – This is hard work…
Interesting though, thanks
Reply
Wait what? The arms of the function fx=x^2 become parallel? That would imply that fx is defined on a finite domain.
Reply
This explanation is jargon-laden and lacks clarity.
It has too many undefined terms: focus, directrix, arms
The graphs are inadequate and lack labels.
The equations are incorrect.
“The parabola is given by the equation y2=X…”—Should be y**2 (or y-squared), and I do not think this is the general equation for a parabola
Grammar problem (missing indefinite article): “Hyperbola is given by the equation XY=1.” This is supposed to be English, not Russian or Korean. And this is not the general equation for a hyperbola, is it?
“When the difference of distances between a set of points present in a plane to two fixed foci or points is a positive constant, it is called a hyperbola.”—Say what?
“We can deal with their differences in a very simple way…”—Oh, really? Prove it.
Wow, great job guyz this help me a lot!—not
Reply
wooow that is great right
Reply
What is this one saying
Reply
woo this is a wonderful thing
Reply
I was able to understand from your explanation but i believe this would be beneficial to more people if you defined the terms BEFORE getting into any explanations..for instance, the 1st paragraph where you mention directrix, focus, axis etc without defining what those words mean seems to be throwing some ppl off.
You do describe the meanings in the following paragraphs of course but by then readers might already feel thrown off.
So maybe put definitions at the very top, switch it where the descriptions are in the 1st paragraph, or even give the descriptions following the terms every time you use the term & also label each image with as many terms as relevant to that image. (For the visual learners)
Not trying to devalue your work bc as i said, I was able to learn from it..just some constructive ideas from the aspect of someone who lacked any knowledge on this subject prior to landing on your page.
Reply
-The “arms” of a parabola do not ever become parallel, though they approach it.
“First of all, when a solid figure, which in this case is a cone, is cut by a plane, the section which is obtained is called a conic section.”
-You can’t just cut any solid figure and get a conic section.
-In a “unit parabola” (I’m not sure what else to call it) the equation is actually Y=X^2, and not Y^2=X (I’m assuming Y2 meant y squared).
-The basic equation for a hyperbola is X^2+Y^2=1, and not XY=1. That equation would make what appears to be a hyperbola tilted 45 degrees but is in fact not.
Reply
Actually you have stated the equation for an ellipse. Change the + sign to a -sign to get a hyperbola
Reply