Difference Between Codomain and Range

Both Codomain and Range are the notions of functions used in mathematics. While both are related to output, the difference between the two is quite subtle. The term “Range” sometimes is used to refer to “Codomain”.  When you distinguish between the two, then you can refer to codomain as the output the function is declared to produce. The term range, however, is ambiguous because it can be sometimes used exactly as Codomain is used. Let’s take f: A -> B, where f is the function from A to B. Then, B is the codomain of the function “f” and range is the set of values that the function takes on, which is denoted by f (A). Range can be equal to or less than codomain but cannot be greater than that.

For example, let A = {1, 2, 3, 4, 5} and B = {1, 4, 8, 16, 25, 64, 125}. The function f: A -> B is defined by f (x) = x ^3. So here,

Domain = Set A

Codomain = Set B, and

Range (R) = {1, 8, 64, 125}

The range should be cube of set A, but cube of 3 (that is 27) is not present in the set B, so we have 3 in domain, but we don’t have 27 either in codomain or range. The range is the subset of the codomain.

What is Codomain of a Function?

The “codomain” of a function or relation is a set of values that might possibly come out of it. It’s actually part of the definition of the function, but it restricts the output of the function. For instance, let’s take the function notation f: R -> R. It means that f is a function from the real numbers to the real numbers. Here, codomain is the set of real numbers R or the set of possible outputs that come out of it. Domain is also the set of real numbers R. Here, you can also specify the function or relation to restrict any negative values that output produces. In simple terms, codomain is a set within which the values of a function fall.

Let N be the set of natural numbers and the relation is defined as R = {(x, y): y = 2x, x, y ∈ N}

Here, x and y both are always natural numbers. So,

Domain = N, and

Codomain = N that is the set of natural numbers.

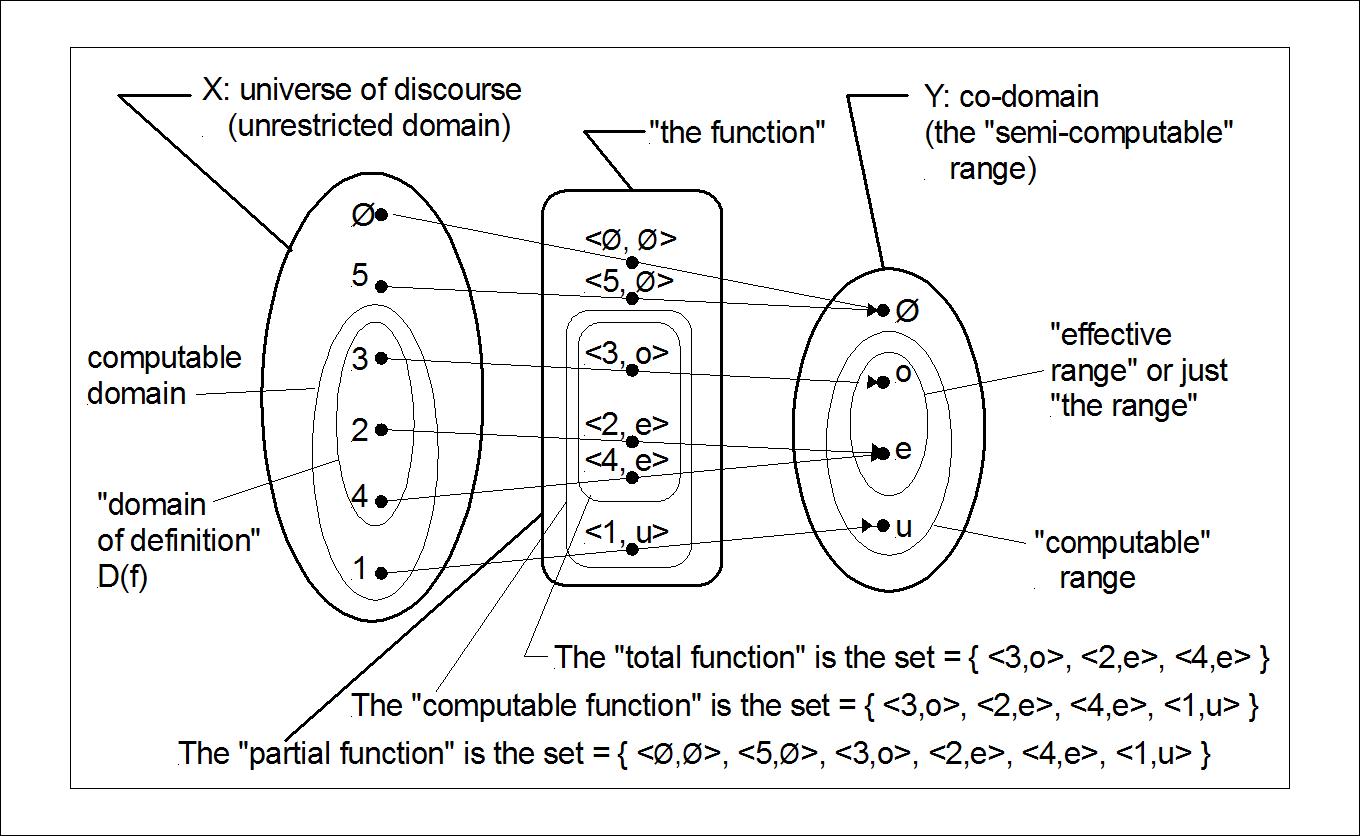
What is Range of a Function?

The “range” of a function is referred to as the set of values that it produces or simply as the output set of its values. The term range is often used as codomain, however, in a broader sense, the term is reserved for the subset of the codomain. In simple terms, range is the set of all output values of a function and function is the correspondence between the domain and the range. In native set theory, range refers to the image of the function or codomain of the function. In modern mathematics, range is often used to refer to image of a function. Older books referred range to what presently known as codomain and modern books generally use the term range to refer to what is currently known as the image. Most books don’t use the word range at all to avoid confusions altogether.

For instance, let A = {1, 2, 3, 4} and B = {1, 4, 9, 25, 64}. The function f: A -> B is defined by f (x) = x ^2. So here, set A is the domain and set B is the codomain, and Range = {1, 4, 9}. The range is the square of A as defined by the function, but the square of 4, which is 16, is not present in either the codomain or the range.

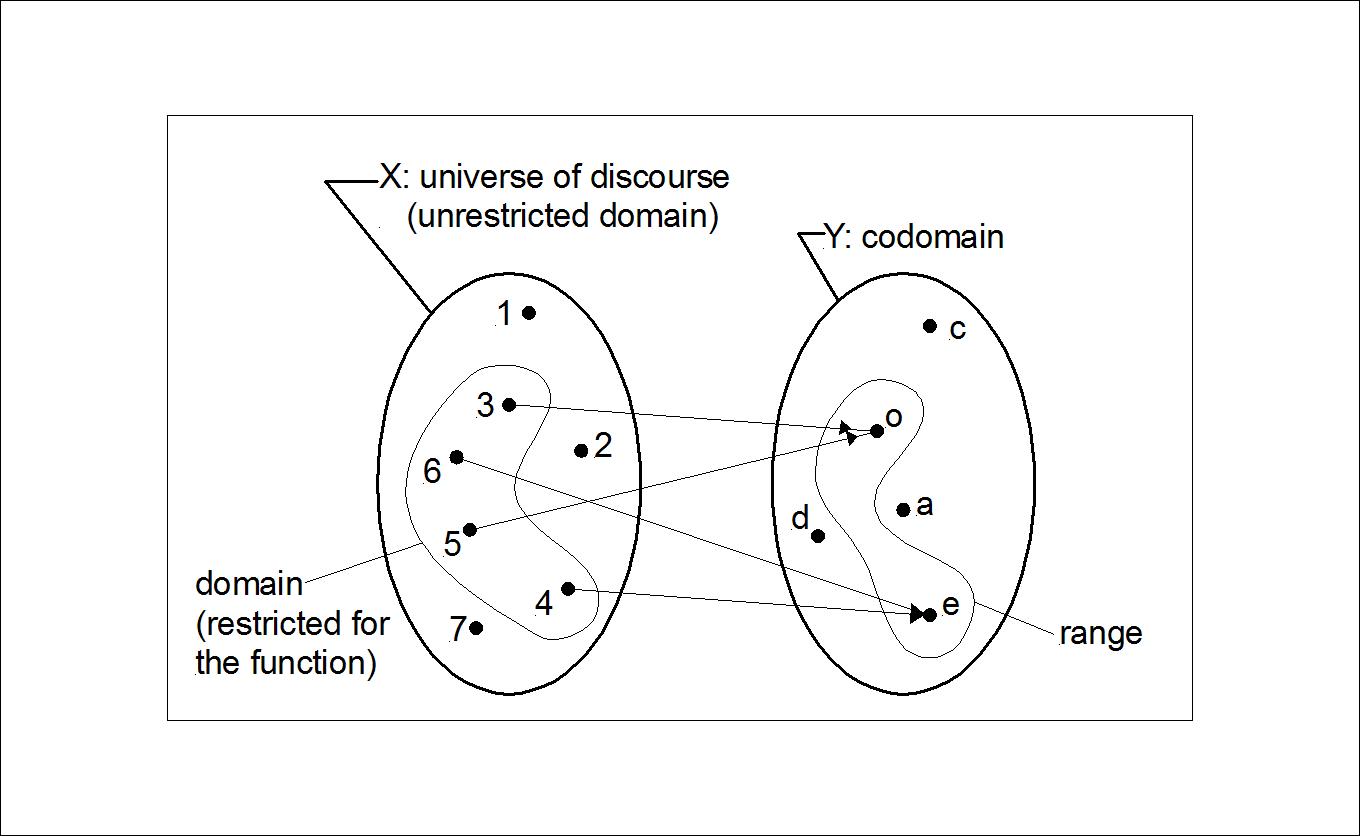
Difference between Codomain and Range

Definition of  Codomain and Range

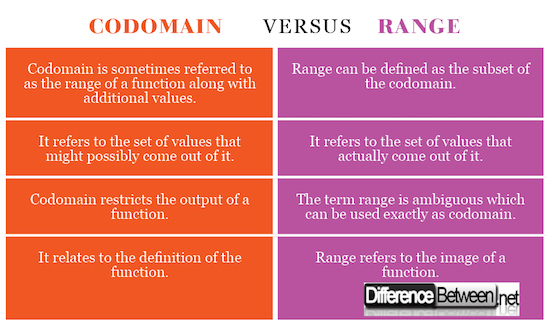
Both the terms are related to output of a function, but the difference is subtle. While codomain of a function is set of values that might possibly come out of it, it’s actually part of the definition of the function, but it restricts the output of the function. Range of a function, on the other hand, refers to the set of values that it actually produces.

Purpose of  Codomain and Range

Codomain of a function is a set of values that includes the range but may include some additional values. The purpose of codomain is to restrict the output of a function. The range can be difficult to specify sometimes, but larger set of values that include the entire range can be specified. The codomain of a function sometimes serves the same purpose as the range.

Example of  Codomain and Range

If A = {1, 2, 3, 4} and B = {1, 2, 3, 4, 5, 6, 7, 8, 9} and the relation f: A -> B is defined by f (x) = x ^2, then codomain = Set B = {1, 2, 3, 4, 5, 6, 7, 8, 9} and Range = {1, 4, 9}. The range is the square of set A but the square of 4 (that is 16) is not present in either set B (codomain) or the range.

Codomain vs. Range: Comparison Chart

Summary of  Codomain vs. Range

While both are common terms used in native set theory, the difference between the two is quite subtle. The codomain of a function can be simply referred to as the set of its possible output values. In mathematical terms, it’s defined as the output of a function. The range of a function, on the other hand, can be defined as the set of values that actually come out of it. However, the term is ambiguous, which means it can be used sometimes exactly as codomain. However, in modern mathematics, range is described as the subset of codomain, but in a much broader sense.

Sharing is caring!