Mathematicians have developed systems to specify how a certain number is different from another. Just like other concepts, number categories overlap. Since real numbers include all rational numbers like the integers, they share similar characteristics such as the utilization of whole numbers and being plotted on the number line. Hence, the key difference is that real numbers is a general classification while integers is a subset which is characterized as whole numbers which can have negative properties.

What are Real Numbers?

Real numbers are the values you can find on the number line which is usually expressed as a geometric horizontal line where a chosen point functions as the “origin”. Those that fall on the right side are labeled as positive while those on the left are negative. The description “real” was presented by Rene Descartes, a famous mathematician and philosopher in the 17th century. He particularly set the difference between Polynomials’ real roots and their imaginary roots.

Real numbers include whole, integers, natural, rational, and irrational numbers:

• Whole numbers

Whole numbers are positive numbers which have no fractional parts nor decimal points as they represent whole objects without fragments or pieces.

• Integers

Integers are whole numbers which include the negative side of the number line.

• Natural numbers

Also known as counting numbers, natural numbers are like whole numbers but zero is not included as nothing can be essentially counted as “0”.

• Rational numbers

Regarding its origins, Pythagoras, the ancient Greek mathematician proclaimed that all numbers were rational. Rational numbers are the quotients or the fractions of two integers.  Where p and q are both integers and q is not equivalent to zero, p/q is a rational number. For instance, 3/5 is a rational number but 3/0 is not.

• Irrational numbers

Pythagoras’ student, Hippasus disagreed that all numbers were rational. Through geometry, he proved that some numbers were irrational. For instance, the square root of two, which is 1.41 cannot be expressed as a fraction; hence, it is irrational. Unfortunately, the actuality of rational numbers was not accepted by the followers of Pythagoras. This resulted to Hippasus’ being drowned at sea which was said to be a punishment from the gods during that time.

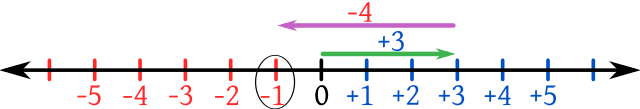
What are Integers?

From the Latin word “integer”, which translates to “whole” or “untouched”, these numbers do not have fractional or decimal components just like whole numbers. The numbers include positive natural numbers or the counting numbers and their negatives. For instance, -3, -2, -1, 0, -1, 2, 3 are integers. The usual illustration are equally spaced numbers on an infinite number line with zero, which is neither positive nor negative, in the middle. Hence, the positives are greater than the negatives.

Regarding its history, the following accounts trace how integers were first utilized:

• In 200 B.C. negative numbers were first represented with red rods in ancient China.
• In around 630 A.D., negative numbers were used to represent debt in India.
• Arbermouth Holst, a German mathematician introduced integers in 1563 as system in addition and multiplication. He developed the system as a response to the increasing number of rabbits and elephants which he was experimenting on.

The following are the characteristics of integers:

• Positive

The numbers at the right side of the number line are positive and they often represent the higher value of their negative counterparts.

• Negative

The numbers at the left side of the number line are often viewed as the lesser standard value of their positive counterparts.

• Neutral

The center of the number line, zero is the integer which is neither positive or negative.

• No fragments

Like whole numbers, integers have no decimal points nor fractions.

Difference between Real Numbers and Integers

Scope of Real Numbers and Integers

Real numbers include integers, rational, irrational, natural, and whole numbers. On the other hand, integers’ scope is mainly concerned with whole numbers which are negative and positive. Hence, real numbers are more general.

Fractions

Real numbers can include fractions such as rational and irrational numbers. However, fractions cannot be integers.

Least-Upper-Bound Property

Real numbers have least-upper-bound-property which is also known as “completeness”. This means that a linear set of real numbers have subsets with supremum qualities.  On the contrary, integers do not have the least-upper-bound property.

Archimedean Property

The Archimedean Property, which is the assumption that there is a natural number that is equal to or greater than any real number, can be applied to real numbers. On the contrary, the Archimedean Property cannot be applied to integers.

Field

Real numbers are a kind of field which is an essential algebraic structure where arithmetic processes are defined. On the contrary, integers are not considered as a field.

Countable

As a set, real numbers are uncountable while integers are countable.

Symbols of Real Numbers and Integers

Real numbers are symbolized as “R” while a set of integers is symbolized as “Z”.  N. Bourbaki, a group of French mathematicians in the 1930s, specified “Z” from the German word “Zahlen” which means number or integers.

Word Origin for Real Numbers and Integers

Real numbers denoted the real roots of a polynomials while integer came from the Latin word, “whole” as they do not include decimals nor fractions.

Real Numbers vs Integers

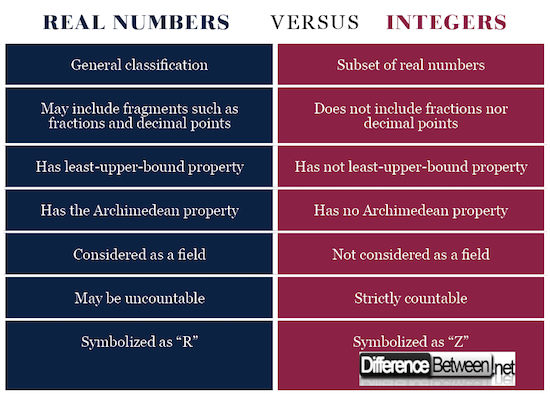
Summary of Real Numbers vs.  Integers

• Both real numbers and integers can be plotted on the number line.
• Integers is a subset of real numbers.
• Integers have negative numbers.
• As a set, real numbers has a more general scope as compared to integers.
• Unlike integers, real numbers may include fractions and decimal points.
• Properties of the least-bound, Archimedean, and field are generally applicable to real numbers but not to integers.
• Unlike real numbers, integers are strictly countable.
• “R” stands for real numbers while “Z” is for integers.

Sharing is caring!